üĒį┤Ż║ą┬└╦Į╠ė² ū„š▀Ż║. 2010-05-09 11:13:20
ĪĪĪĪ
ĪĪĪĪ
ĪĪĪĪ
ĪĪĪĪ╝tś“ģ^Š┼─Ļ╝ēę╗─����Ż┐╝įćäéäéĮY╩°����Ż¼ėąĄ─īW╔·š²│┴Į■ė┌▀M▓ĮĄ─Ž▓Ééųą�Ż¼ī”ųą┐╝│õØM┴╦ą┼ą─;Č°ėąĄ─īW╔·š²×ķ│╔┐āĄ─═╦▓Į╗“═Ż£■▓╗Ū░Č°Š┌å╩Ż¼├µī”ųą┐╝Ż¼╩¦╚ź┴╦ČĘųŠĪŻ═©▀^šJšµĘų╬÷įćŅ}��ĪóĘų╬÷īW╔·��Ż¼╬ęéā░l¼F╩╣īW╔·ĖąĄĮ└¦ļy����ĪóīW╔·Õeš`┬╩▌^Ė▀Ą─Ņ}─┐���Ż¼ę╗ĘĮ├µ┐╝▓ķīW╔·į·īŹĄ─╗∙▒Š╣”�����Ż¼┴Ēę╗ĘĮ├µąĶę¬īW╔·Š▀ėą╝Ü─üĄ─╦╝ŠS��ĪŻ╦ūįÆšfŻ║┼_╔Žę╗ĘųńŖŻ¼┼_Ž┬╩«─Ļ╣”ĪŻę¬Žļ┐╝ł÷╔Žėąņ`├¶Ą─Ę┤æ¬�����Ż¼╣żĘ“ꬎ┬į┌ŲĮĢr�ĪŻŽ┬├µ�����Ż¼╬ęéāŠ═×ķ┤¾╝ęųvĮŌŽÓ╦Ų╚²ĮŪą╬▓┐Ęų╚ń║╬ūC├„����Ż¼ŽŻ═¹─▄ē“Ä═ų·═¼īWéāĮŌøQŲ╚²ĮŪą╬ŽÓ╦Ųå¢Ņ}üĒ�����Ż¼╚ļ╩ų┐ņ��ĪóĘĮĘ©Ū╔ĪŻ
ĪĪĪĪį┌ŽÓ╦Ų╚²ĮŪą╬ę╗š┬╣ØĄ─Å═┴Ģųą����Ż¼╬ęéā┐╔ęį┐éĮYę╗ą®│Żė├Ą─ŽÓ╦Ų╚²ĮŪą╬Ą─“╗∙▒ŠłDą╬╦ž▓─”����Ż¼╝┤╩╣├µī”Å═ļsĄ─łDą╬�Ż¼╬ęéā┐╔ęįÅ─ųą░l¼F╩ņų¬Ą─╗∙▒ŠłDą╬Ż¼īółDą╬▀MąąĘųĮŌ���Ż¼─▄ē“Ä═ų·─ŃčĖ╦┘ĄžšęĄĮ╚ļ╩ų³cĪŻŽ┬├µ╬ęéāęį│Żė├Ą─╦─éĆŽÓ╦Ų╚²ĮŪą╬Ą─╗∙▒ŠłDą╬×ķ└²�����Ż¼Ä═ų·─Ń¾wĢ■╦³éāĄ─ųžę¬ū„ė├���ĪŻ
ĪĪĪĪ¼Fęį╝tś“ģ^Ą─ę╗Ą└┐╝Ņ}×ķ└²����Ż¼Ęų╬÷īW╔·Ą─Õeš`įŁę“╝░╗∙▒ŠłDą╬ų«ķgĄ─▓Ņ«ÉĪŻ
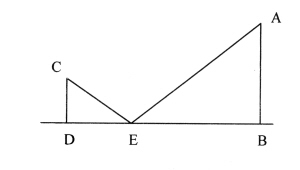
ĪĪĪĪ═§Ę╝═¼īW└¹ė├Ž┬├µĄ─ĘĮĘ©£y┴┐īWąŻŲņŚUĄ─Ė▀�ĪŻ╚ńłDį┌ŲņŚUĄ─Ąū▓┐Bę²ę╗Ślų▒ŠĆBM�Ż¼į┌▀@Ślų▒ŠĆ▀m«öĄ─╬╗ų├E╠ÄĘ┼ę╗├µńRūė�Ż¼«ö╦²čžų°▀@Ślų▒ŠĆū▀ĄĮ³cD╠ÄĢrŪĪ║├į┌ńRūėųą┐┤ĄĮŲņŚUĄ─ĒöČ╦AŻ¼ėų£yĄ├BE=18├ū�����Ż¼ED=2.4├ū�����Ż¼ęčų¬═§Ę╝Ą─č█Š”ĄĮĄž├µĄ─Ė▀Č╚CD=1.6├ū�ĪŻ
ĪĪĪĪšł─Ń╠µ═§Ę╝═¼īWėŗ╦Ń│÷ŲņŚUABĖ▀���ĪŻ
ĪĪĪĪĪŠÕeš`1Ī┐Ī▀CDĪ╬AB
ĪĪĪĪ∴Ī„CDEĪūĪ„ABE
ĪĪĪĪĪŠĘų╬÷Ī┐įō╔·īó┤╦łD┼cŲĮąą→ŽÓ╦Ųųą“X”ą═╗ņŽ²┴╦����ĪŻ
ĪĪĪĪ╚ńłD(1)Ż║CDĪ╬ABŻ¼ė^▓ņłDą╬����Ż¼╬ęéāĢ■░l¼FĪ„CDE┼cĪ„BAEŠ▀ėąę╗ĮMī”ĒöĮŪ�ĪŻ
ĪĪĪĪ▒╚▌^ā╔éĆłDą╬��Ż¼’@╚╗�����Ż¼┐╝Ņ}Ą─łDą╬ųąĪ„CDE┼cĪ„ABE▓╗┤µį┌ī”ĒöĮŪŻ¼īW╔·į┌ĮŌŅ}▀^│╠ųąš²╩Ūīó▀@ā╔éĆŠ▀ėą▓╗═¼╠žš„Ą─łDą╬╗ņŽ²┴╦���Ż¼▓┼ū÷│÷┴╦Õeš`Ą─ĮŌĘ©���ĪŻ
ĪĪĪĪĪŠš²┤_ĮŌĘ©Ī┐┤╦łDąĶę¬▀\ė├╣ŌīWų¬ūRųąĄ─“Ę┤╔õĮŪŽÓĄ╚”→
ĪĪĪĪ∠CED=∠AEB
ĪĪĪĪĪ▀CD⊥BDė┌D��Ż¼AB⊥BDė┌B
ĪĪĪĪ∴∠CDE=∠ABE=90°
ĪĪĪĪėųĪ▀ė╔╣ŌīWų¬ūRĄ├∠CED=∠AEB
ĪĪĪĪ∴Ī„CDEĪūĪ„ABE
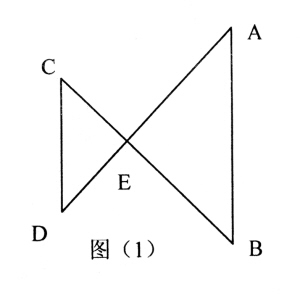
ĪĪĪĪĪŠÕeš`2Ī┐Ī▀Ī„CDEĪūĪ„EBA
ĪĪĪĪ∴AB:DE=BE:CD
ĪĪĪĪĪŠĘų╬÷Ī┐īW╔·īó┐╝Ņ}Ą─łDą╬┼cłDą╬(2)░l╔·┴╦╗ņŽ²�ĪŻ
ĪĪĪĪ╚ńłD(2)Ż║AB⊥BDė┌B���Ż¼CD⊥BDė┌D��Ż¼AE⊥CEė┌E����Ż¼Š▀ėą╚²éĆ╠ž╩ŌĮŪ�Ż¼ė╔ėÓĮŪĄ─ąį┘|┐╔═ŲĄ├∠C=∠AEBŻ¼∠CED=∠AŻ¼ā╔éĆŽÓ╦Ų╚²ĮŪą╬ę╗╠╔ę╗┴ó;Č°┐╝Ņ}łDųąät╩Ū∠CED=∠AEB�Ż¼∠C=∠A��Ż¼ā╔éĆŽÓ╦Ų╚²ĮŪą╬├µī”├µĘ┼ų├ĪŻ
ĪĪĪĪīW╔·į┌ĮŌŅ}▀^│╠ųą��Ż¼ė╔ė┌║÷ęĢ┴╦ā╔éĆłDą╬ų«ķgĄ─╝Ü╬ó▓Ņ«É����Ż¼Å─Č°ī¦ų┬┴╦Õeš`▒╚└²╩ĮĄ─Ģ°īæĪŻ
ĪĪĪĪĪŠš²┤_ĮŌĘ©Ī┐
ĪĪĪĪĪ▀Ī„CDEĪūĪ„ABE
ĪĪĪĪ∴AB:CD=BE:DE
ĪĪĪĪĪŠ═Ļš¹ĮŌĘ©Ī┐Ī▀CD⊥BDė┌DŻ¼AB⊥BDė┌B
ĪĪĪĪ∴∠CDE=∠ABE=90°
ĪĪĪĪėųĪ▀ė╔╣ŌīWų¬ūRĄ├∠CED=∠AEB
ĪĪĪĪ∴Ī„CDEĪūĪ„ABE
ĪĪĪĪ∴AB:CD=BE:DE
ĪĪĪĪ∴AB:1.6=18:2.4 ∴AB=12
ĪĪĪĪ┤Ż║ŲņŚUABĖ▀×ķ12├ū�ĪŻ
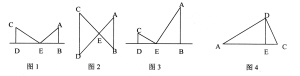
ĪĪĪĪ═©▀^Ęų╬÷ā╔ĘNÕeš`ĮŌĘ©�Ż¼╬ęéā░l¼FīW╔·éāėąŽÓ╦Ų╚²ĮŪą╬╗∙▒ŠłDą╬Ą─ėĪŽ¾���Ż¼ģs║÷ęĢ┴╦╗∙▒ŠłDą╬1��Īó2�����Īó3ų«ķgĄ─ģ^äe���Ż¼░l╔·┴╦╗ņŽ²�ĪŻę“┤╦Ż¼╬ęéā▓╗āHę¬░l¼F��ĪóÜw╝{╗∙▒ŠłDą╬�Ż¼Ė³ę¬ĻPūó╦³éāų«ķgĄ─ģ^äe┼c┬ōŽĄŻ¼ęį▒Ńį┌ĮŌŅ}▀^│╠ųą▒▄├Ō╩¦š`��Īó░lō]Ė³┤¾Ą─╣”ą¦���ĪŻ
ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖCĪóŲĮ░ÕĄ╚ęŲäėįOéõįLå¢ųą┐╝ŠW�Ż¼2024ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą���ŻĪ>>³cō¶▓ķ┐┤












