平行四邊形是一種極重要的幾何圖形.這不僅是因?yàn)樗茄芯扛厥獾钠叫兴倪呅唯D―矩形、菱形、正方形的基礎(chǔ),還因?yàn)橛伤亩x知它可以分解為一些全等的三角形,并且包含著有關(guān)平行線的許多性質(zhì),因此,它在幾何圖形的研究上有著廣泛的應(yīng)用.
由平行四邊形的定義決定了它有以下幾個(gè)基本性質(zhì):
(1)平行四邊形對(duì)角相等;
(2)平行四邊形對(duì)邊相等;
(3)平行四邊形對(duì)角線互相平分.
除了定義以外,平行四邊形還有以下幾種判定方法:
(1)兩組對(duì)角分別相等的四邊形是平行四邊形;
(2)兩組對(duì)邊分別相等的四邊形是平行四邊形;
(3)對(duì)角線互相平分的四邊形是平行四邊形;
(4)一組對(duì)邊平行且相等的四邊形是平行四邊形.
例1 如圖2-32所示.在 ABCD中,AE⊥BC,CF⊥AD,DN=BM.求證:EF與MN互相平分.
ABCD中,AE⊥BC,CF⊥AD,DN=BM.求證:EF與MN互相平分.
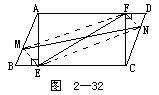
分析 只要證明ENFM是平行四邊形即可,由已知,提供的等量要素很多,可從全等三角形下手.
證 因?yàn)?/FONT>ABCD是平行四邊形,所以
AD BC,AB
BC,AB CD,∠B=∠D.
CD,∠B=∠D.
又AE⊥BC,CF⊥AD,所以AECF是矩形,從而
AE=CF.
所以
Rt△ABE≌Rt△CDF(HL,或AAS),BE=DF.又由已知BM=DN,所以
△BEM≌△DFN(SAS),
ME=NF. ①
又因?yàn)?/FONT>AF=CE,AM=CN,∠MAF=∠NCE,所以
△MAF≌△NCE(SAS),
所以 MF=NF. ②
由①,②,四邊形ENFM是平行四邊形,從而對(duì)角線EF與MN互相平分.
例2 如圖2-33所示.Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC且交AC于F.求證:AE=CF.
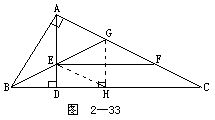
分析 AE與CF分處于不同的位置,必須通過(guò)添加輔助線使兩者發(fā)生聯(lián)系.若作GH⊥BC于H,由于BG是∠ABC的平分線,故AG=GH,易知△ABG≌△HBG.又連接EH,可證△ABE≌△HBE,從而AE=HE.這樣,將AE“轉(zhuǎn)移”到EH位置.設(shè)法證明EHCF為平行四邊形,問(wèn)題即可獲解.
證 作GH⊥BC于H,連接EH.因?yàn)?/FONT>BG是∠ABH的平分線,GA⊥BA,所以GA=GH,從而
△ABG≌△HBG(AAS),
所以 AB=HB. ①
在△ABE及△HBE中,
∠ABE=∠CBE,BE=BE,
所以 △ABE≌△HBE(SAS),
所以 AE=EH,∠BEA=∠BEH.
下面證明四邊形EHCF是平行四邊形.
因?yàn)?/FONT>AD∥GH,所以
∠AEG=∠BGH(內(nèi)錯(cuò)角相等). ②
又∠AEG=∠GEH(因?yàn)椤?/FONT>BEA=∠BEH,等角的補(bǔ)角相等),∠AGB=∠BGH(全等三角形對(duì)應(yīng)角相等),所以
∠AGB=∠GEH.
從而
EH∥AC(內(nèi)錯(cuò)角相等,兩直線平行).
由已知EF∥HC,所以EHCF是平行四邊形,所以
FC=EH=AE.
說(shuō)明 本題添加輔助線GH⊥BC的想法是由BG為∠ABC的平分線的信息萌生的(角平分線上的點(diǎn)到角的兩邊距離相等),從而構(gòu)造出全等三角形ABG與△HBG.繼而發(fā)現(xiàn)△ABE≌△HBE,完成了AE的位置到HE位置的過(guò)渡.這樣,證明EHCF是平行四邊形就是順理成章的了.
人們?cè)趯W(xué)習(xí)中,經(jīng)過(guò)刻苦鉆研,形成有用的經(jīng)驗(yàn),這對(duì)我們探索新的問(wèn)題是十分有益的.
例3 如圖2-34所示.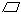 ABCD中,DE⊥AB于E,BM=MC=DC.求證:∠EMC=3∠BEM.
ABCD中,DE⊥AB于E,BM=MC=DC.求證:∠EMC=3∠BEM.
分析 由于∠EMC是△BEM的外角,因此∠EMC=∠B+∠BEM.從而,應(yīng)該有∠B=2∠BEM,這個(gè)論斷在△BEM內(nèi)很難發(fā)現(xiàn),因此,應(yīng)設(shè)法通過(guò)添加輔助線的辦法,將這兩個(gè)角轉(zhuǎn)移到新的位置加以解決.利用平行四邊形及M為BC中點(diǎn)的條件,延長(zhǎng)EM與DC延長(zhǎng)線交于F,這樣∠B=∠MCF及∠BEM=∠F,因此, 只要證明∠MCF=2∠F即可.不難發(fā)現(xiàn),△EDF為直角三角形(∠EDF=90°)及M為斜邊中點(diǎn),我們的證明可從這里展開(kāi).
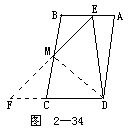
證 延長(zhǎng)EM交DC的延長(zhǎng)線于F,連接DM.由于CM=BM,∠F=∠BEM,∠MCF=∠B,所以
△MCF≌△MBE(AAS),
所以M是EF的中點(diǎn).由于AB∥CD及DE⊥AB,所以,DE⊥FD,三角形DEF是直角三角形,DM為斜邊的中線,由直角三角形斜邊中線的性質(zhì)知
∠F=∠MDC,
又由已知MC=CD,所以
∠MDC=∠CMD,
則
∠MCF=∠MDC+∠CMD=2∠F.
從而
∠EMC=∠F+∠MCF=3∠F=3∠BEM.
例4 如圖2-35所示.矩形ABCD中,CE⊥BD于E,AF平分∠BAD交EC延長(zhǎng)線于F.求證:CA=CF.
分析 只要證明△CAF是等腰三角形,即∠CAF=∠CFA即可.由于∠CAF=45°-∠CAD,所以,在添加輔助線時(shí),應(yīng)設(shè)法產(chǎn)生一個(gè)與∠CAD相等的角a,使得∠CFA=45°-a.為此,延長(zhǎng)DC交AF于H,并設(shè)AF與BC交于G,我們不難證明∠FCH=∠CAD.
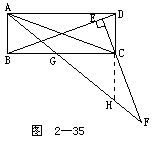
證 延長(zhǎng)DC交AF于H,顯然∠FCH=∠DCE.又在Rt△BCD中,由于CE⊥BD,故∠DCE=∠DBC.因?yàn)榫匦螌?duì)角線相等,所以△DCB≌△CDA,從而∠DBC=∠CAD,因此,
∠FCH=∠CAD. ①
又AG平分∠BAD=90°,所以△ABG是等腰直角三角形,從而易證△HCG也是等腰直角三角形,所以∠CHG=45°.由于∠CHG是△CHF的外角,所以
∠CHG=∠CFH+∠FCH=45°,
所以 ∠CFH=45°-∠FCH. ②
由①,②
∠CFH=45°-∠CAD=∠CAF,
于是在三角形CAF中,有
CA=CF.
例5 設(shè)正方形ABCD的邊CD的中點(diǎn)為E,F是CE的中點(diǎn)(圖2-36).求證:
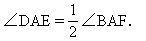
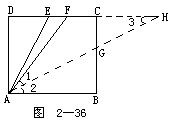
分析 作∠BAF的平分線,將角分為∠1與∠2相等的兩部分,設(shè)法證明∠DAE=∠1或∠2.
證 如圖作∠BAF的平分線AH交DC的延長(zhǎng)線于H,則∠1=∠2=∠3,所以
FA=FH.
設(shè)正方形邊長(zhǎng)為a,在Rt△ADF中,
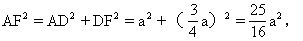
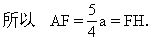
從而
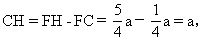
所以 Rt△ABG≌Rt△HCG(AAS),
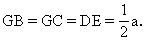
從而
Rt△ABG≌Rt△ADE(SAS),
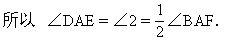
例6 如圖2-37所示.正方形ABCD中,在AD的延長(zhǎng)線上取點(diǎn)E,F,使DE=AD,DF=BD,連接BF分別交CD,CE于H,G.求證:△GHD是等腰三角形.
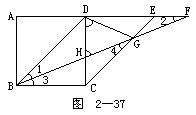
分析 準(zhǔn)確地畫圖可啟示我們證明∠GDH=∠GHD.
證 因?yàn)?/FONT>DE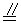 BC,所以四邊形BCED為平行四邊形,所以∠1=∠4.又BD=FD,所以
BC,所以四邊形BCED為平行四邊形,所以∠1=∠4.又BD=FD,所以
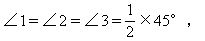
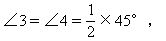
所以 BC=GC=CD.
因此,△DCG為等腰三角形,且頂角∠DCG=45°,所以
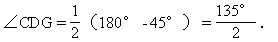
又
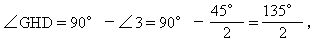
所以 ∠HDG=∠GHD,
從而GH=GD,即△GHD是等腰三角形.
練習(xí)十二
1.如圖2-38所示.DE⊥AC,BF⊥AC,DE=BF,∠ADB=∠DBC.求證:四邊形ABCD是平行四邊形.
2.如圖2-39所示.在平行四邊形ABCD中,△ABE和△BCF都是等邊三角形.求證:△DEF是等邊三角形.


3.如圖2-40所示. ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求證:BE=CF.
ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求證:BE=CF.
4.如圖2-41所示.矩形ABCD中,F在CB延長(zhǎng)線上,AE=EF,CF=CA.求證:BE⊥DE.
5.如圖2-42所示.在正方形ABCD中,CE垂直于∠CAB的平分



歡迎使用手機(jī)、平板等移動(dòng)設(shè)備訪問(wèn)中考網(wǎng),2024中考一路陪伴同行!>>點(diǎn)擊查看









