8.7　捷徑

　　我們都知道，光在同一種介質里的傳播是依直線進行的，也就是說是依最近的路徑進行的。但是，當光從一點射出不是直接射到另一點，而是經過鏡面的反射射到另一點的時候，光也仍舊是依最短的路徑進行的。

　　讓我們跟著光的路徑看去。假設圖93上A點表示光源，MN線表示鏡面，ABC線表示光從蠟燭到人的眼睛C的路徑。直線KB跟MN垂直。

　　根據光學的定律，反射角2等于入射角1。知道了這一點，就很容易證明從A點到鏡面再到C點的所有可能走的路線里，ABC是最短的一條。這我們可以把光線的路徑ABC跟另外一條路徑比如ADC來比較一下。從A點向MN作一垂線AE，把它延長到跟CB線的延長線相交于 F。然后把F、D兩點用直線連接起來。首先讓我們證明三角形ABE和 FBE全等。這兩個三角形都是直角三角形，而且有公共的直角邊EB；此外，EFB和EAB兩角相等，因為它們分別跟角2和角1相等；這樣就證明了兩個三角形ABE和FBE全等。于是得到AB=FB，AE=FE。現在再來看兩個直角三角形ADE和FDE，它們有公共的直角邊ED，又上面已經證明AE=FE，所以兩個三角形ADE和FDE也全等。因此，AD和 FD也自然相等。

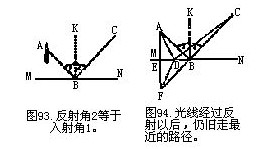
　　這樣一來，我們可以把路線ABC用跟它相等的路線FBC來代替（因為AB=FB），把路線ADC用路線FDC來代替。把這兩條路線 FBC跟FDC比較，可見直線 FBC要比折線FDC短。因此，路線 ABC要比ADC短，而這正是我們需要證明的！

　　無論D點在什么地方，只要反射角等于入射角，路線ABC總比路線ADC短。這樣，光線在光源、鏡子和人的眼睛之間進行，果然是選擇所有可能的路線里最短的一條。這一點，還在第二世紀時候就由希臘的機械師和數學家亞歷山大城的希羅指出了。

　　 歡迎使用手機、平板等移動設備訪問中考網，2023中考一路陪伴同行！>>點擊查看