第二章力·功·摩擦 2.6儒勒·凡爾納的大力士和歐拉的公式

　　你記得儒勒·凡爾納書里的競技大力士馬蒂夫嗎？“頭大身高，胸膛象鐵匠的風囊，腿象粗壯的木柱，胳膊象起重機，拳頭象鐵錘……”這位大力士的功勞在《馬蒂斯·桑多爾夫》這部小說里敘述得很多，可是使讀者印象最深的，大概是他用手拉住一條正在下水的船“特拉波科羅”號這件事。

　　關于這件事，小說的作者是這樣告訴我們的。

　　已經移去了在兩旁撐住船身的支持物，船準備下水了。只要把纜索解開，船就會滑下去。已經有五六個木工在船的龍骨底下忙著。觀眾滿懷著好奇心注視著這件工作。這時候，卻有一只快艇繞過岸邊凸出的地方，出現在人們眼前。原來這只快艇要進港口，必須經過“特拉波科羅”號準備下水的船塢前面。所以一聽見快艇發出信號，大船上的人為了避免發生意外，就停止了解纜下水的操作，讓快艇先過去。假使這兩條船，一條橫著，另一條用極高的速度沖過去，快艇一定會被撞沉的。

　　工人們停止了錘擊。所有的眼睛全都注視著這只華麗的船。船上的白色篷帆在斜陽下象鍍了金一樣。快艇很快就出現在船塢的正前面。船塢上成千的人都出神地看著它。突然聽到一聲驚呼，“特拉波科羅”號正當快艇的右舷對著它的時侯，開始搖擺著滑下去了。兩條船就要相撞了。已經沒有時間、沒有方法能夠防止這場慘禍了。“特拉波科羅”號很快地斜著向下面滑去……船頭上卷起了因摩擦而起的白霧，船尾已經沒入了水①。

　　突然出現了一個人，他抓住了掛在“特拉波科羅”號前部的纜索，用力地拉，幾乎把身子彎得接近了地面。不到一分鐘，他巳經把纜索繞在釘在地里的鐵樁上。他冒著被摔死的危險，用超人的氣力，用手拉住纜索大約有十秒鐘。最后，纜索斷了。可是這十秒鐘時間已經很足夠：“特拉波科羅”號進水以后，只輕微地擦了一下快艇，就向前駛了開去。

　　快艇已經脫了險。至于這個使這件發生得很快的意外事件沒有造成慘禍的人——當時甚至別人來不及幫助他——就是馬蒂夫。

　　假使小說的作者聽到說，這樣的功勞并不需要一個象馬蒂夫那樣的“力大如虎”的巨人，而是每一個機智的人都能干的話，那他一定會非常驚奇。

　　力學告訴我們，纏在樁上的繩索，在滑動的時候，摩擦力可以達到極大的程度。繩索繞的圈數越多，摩擦力也就越大。摩擦力增長的規律是：如果圈數按照算術級數加多，摩擦力就按照幾何級數增長。所以就是一個小孩子，只要能把繩索在一個不動的轆轤上繞三四圈，然后抓住繩頭，他的力量就能平衡一個極大的重物。在河邊的輪船碼頭上，常常有一些少年，就用這個方法使載著幾百個乘客的輪船靠碼頭。原來在這里幫助他們的，并不是他們異常的臂力，而是繩和樁子之間的摩擦力。

　　十八世紀著名數學家歐拉，曾經確定了摩擦力跟繩索繞在樁子上的圈數之間的關系。我現在把歐拉的有用的公式引在下面，給那些不怕簡潔的代數語言的讀者參考：

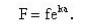
　　在這個公式里，f代表我們所用的力，F代表我們所要對抗的力。e代表數2.718……（自然對數的底），k代表繩和樁子之間的摩擦系數。α代表繞轉角，也就是繩索繞成的弧的長度跟弧的半徑的比。

　　把這個公式應用在儒勒·凡爾納的故事里，所得的結果非常使人吃驚。這里，力F是沿著船塢滑下去的船對纜索的拉力。從小說里我們知道，船的重量是50噸。假定船塢的坡度是1／10，那末，作用在纜索上的就不是船的全重，而是全重的十分之一，也就是5噸或5000公斤。

　　再說，把k——纜索和鐵樁之間的摩擦系數——的數值算做1／3。α的數值是不難計算的。如果我們假定馬蒂夫曾經把纜索繞樁三圈。這時候：

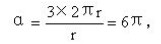
　　把這些數值代進歐拉的公式，就可以得到：

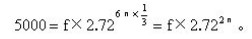
　　未知數f（就是需要的人力）可以用對數求出來：

log5000＝logf＋2πlog2.72，

　　得到 f＝9.3公斤。

　　因此，這個大力士只要用10公斤力氣就可以把纜索拉住，立下這次大功了！

　　你別以為這個數值——10公斤——不過是理論上的，實際需要的一定比這大得多。恰恰相反，這個數對我們說來已經太大了：古時候用來系船的是麻繩和木柱，在這兩種東西之間，摩擦系數k比上面所用的數值更大，所以所需要的力量簡直小得可笑。只要繩索夠牢，吃得住拉力，就是力氣小的孩子，把它套在柱上繞三四圈以后，也能同樣立下這個儒勒·凡爾納小說里的大力士所立的功勞，或者還能勝過他哩。
 

　　 歡迎使用手機、平板等移動設備訪問中考網，2023中考一路陪伴同行！>>點擊查看