知識點總結
一、特殊的平行四邊形
1.矩形:
(1)定義:有一個角是直角的平行四邊形。
(2)性質:矩形的四個角都是直角;矩形的對角線平分且相等。
(3)判定定理:
①有一個角是直角的平行四邊形叫做矩形。②對角線相等的平行四邊形是矩形。③有三個角是直角的四邊形是矩形。
直角三角形的性質:直角三角形中所對的直角邊等于斜邊的一半。
2.菱形:
(1)定義 :鄰邊相等的平行四邊形。
(2)性質:菱形的四條邊都相等;菱形的兩條對角線互相垂直,并且每一條對角線平分一組對角。
(3)判定定理:
①一組鄰邊相等的平行四邊形是菱形。
②對角線互相垂直的平行四邊形是菱形。
③四條邊相等的四邊形是菱形。
(4)面積:
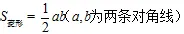
3.正方形:
(1)定義:一個角是直角的菱形或鄰邊相等的矩形。
(2)性質:四條邊都相等,四個角都是直角,對角線互相垂直平分。 正方形既是矩形,又是菱形。
(3)正方形判定定理:
①對角線互相垂直平分且相等的四邊形是正方形;
②一組鄰邊相等,一個角為直角的平行四邊形是正方形;
③對角線互相垂直的矩形是正方形;
④鄰邊相等的矩形是正方形
⑤有一個角是直角的菱形是正方形;
⑥對角線相等的菱形是正方形。
二、矩形、菱形、正方形與平行四邊形、四邊形之間的聯系:
1.矩形、菱形和正方形都是特殊的平行四邊形,其性質都是在平行四邊形的基礎上擴充來的。矩形是由平行四邊形增加“一個角為90°”的條件得到的,它在角和對角線方面具有比平行四邊形更多的特性;菱形是由平行四邊形增加“一組鄰邊相等”的條件得到的,它在邊和對角線方面具有比平行四邊形更多的特性;正方形是由平行四邊形增加“一組鄰邊相等”和“一個角為90°”兩個條件得到的,它在邊、角和對角線方面都具有比平行四邊形更多的特性。
2.矩形、菱形的判定可以根據出發點不同而分成兩類:一類是以四邊形為出發點進行判定,另一類是以平行四邊形為出發點進行判定。而正方形除了上述兩個出發點外,還可以從矩形和菱形出發進行判定。
三、判定一個四邊形是特殊四邊形的步驟:
常見考法
(1)利用菱形、矩形、正方形的性質進行邊、角以及面積等計算;
(2)靈活運用判定定理證明一個四邊形(或平行四邊形)是菱形、矩形、正方形;
(3)一些折疊問題;
(4)矩形與直角三角形和等腰三角形有著密切聯系、正方形與等腰直角三角形也有著密切聯系。所以,以此為背景可以設置許多考題。
誤區提醒
(1)平行四邊形的所有性質矩形、菱形、正方形都具有,但矩形、菱形、正方形具有的性質平行四邊形不一定具有,這點易出現混淆;
(2)矩形、菱形具有的性質正方形都具有,而正方形具有的性質,矩形不一定具有,菱形也不一定具有,這點也易出現混淆;
(3)不能正確的理解和運用判定定理進行證明,(如在證明菱形時,把四條邊相等的四邊形是菱形誤解成兩組鄰邊相等的四邊形是菱形);(3)再利用對角線長度求菱形的面積時,忘記乘;(3)判定一個四邊形是特殊的平行四邊形的條件不充分。
【典型例題】(2010天門、潛江、仙桃)正方形ABCD中,點O是對角線DB的中點,點P是DB所在直線上的一個動點,PE⊥BC于E,PF⊥DC于F.
(1)當點P與點O重合時(如圖①),猜測AP與EF的數量及位置關系,并證明你的結論;
(2)當點P在線段DB上 (不與點D、O、B重合)時(如圖②),探究(1)中的結論是否成立?若成立,寫出證明過程;若不成立,請說明理由;
(3)當點P在DB的長延長線上時,請將圖③補充完整,并判斷(1)中的結論是否成立?若成立,直接寫出結論;若不成立,請寫出相應的結論.
【解析】(1)AP=EF,AP⊥EF,理由如下:
連接AC,則AC必過點O,延長FO交AB于M;
∵OF⊥CD,OE⊥BC,且四邊形ABCD是正方形,
∴四邊形OECF是正方形,
∴OM=OF=OE=AM,
∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,
∴△AMO≌△FOE,
∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,
故AP=EF,且AP⊥EF.
(2)題(1)的結論仍然成立,理由如下:
延長AP交BC于N,延長FP交AB于M;
∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,
∴四邊形MBEP是正方形,
∴MP=PE,∠AMP=∠FPE=90°;
又∵AB-BM=AM,BC-BE=EC=PF,且AB=BC,BM=BE,
∴AM=PF,
∴△AMP≌△FPE,
∴AP=EF,∠APM=∠FPN=∠PEF
∵∠PEF+∠PFE=90°,∠FPN=∠PEF,
∴∠FPN+∠PFE=90°,即AP⊥EF,
故AP=EF,且AP⊥EF.
(3)題(1)(2)的結論仍然成立;
如右圖,延長AB交PF于H,證法與(2)完全相同
歡迎使用手機、平板等移動設備訪問中考網,2023中考一路陪伴同行!>>點擊查看