來源:網絡資源 2022-10-15 10:51:21
在平面直角坐標系中,求一個三角形面積,需要根據三角形的各頂點的坐標,確定底與高,進而求出三角形面積。其它不規則的多邊形經常通過割補轉化成三角形或可以計算的四邊形(矩形,梯形等)來計算面積。例如可以把四邊形分割成兩個三角形來計算(五邊形可以分割成3個三角形,n邊形可以分割成n-2個三角形)。所以最基礎最重要的就是三角形面積的計算!
三角形的面積計算
(一)有邊與坐標軸平行時,可以直接計算三角形面積。
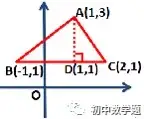
如上圖,因為有邊與坐標軸平行,所以這條邊的長度,和這條邊上的高就非常容易計算,底BC=2-(-1)=3,高AD=3-1=2,之后可以直接計算△ABC的面積。
(二)當三角形是一個斜三角形
①鉛錘法(三角形面積=水平寬×鉛錘高÷2)
過點A作AD垂直于x軸,交BC于點D,則AD叫做鉛錘高。點D的橫坐標與A相同,縱坐標可以利用直線AD與直線BC求得,之后可以得到AD的長度。
過點B與點C作x軸的垂線,兩條垂線的距離叫做水平寬。
其原理就是把△ABC分割成兩個以AD為底的兩個三角形:△ABD與△CAD,它倆的高的和就是水平寬w,所以S△ABC=S△ABD+S△CAD=hw/2

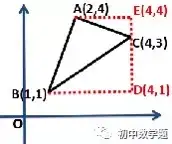
②補成梯形,過三個頂點作x軸與y軸的垂線。
用S梯形ABDE-S△CEA-S△BDC
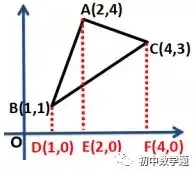
③也可以通過重組轉化成直角梯形面積的和與差。例如下圖,S△ABC=S梯形ABDE+S梯形CAEF-S梯形CBDF
方法很多,可根據題的特點和已知條件來靈活選擇解法。
多邊形
(一)分割成三角形或可以計算的四邊形(梯形等)
如圖所示,四邊形ABCD中,A(2,4),B(1,2),C(3,1),D(5,3),求四邊形ABCD的面積。例如:S四邊形ABCD=S△ABC+S△ACD
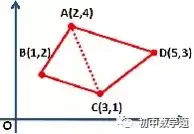
(二)也可以圍補成可以計算的四邊形,此處補成長方形再減去4個容易計算的直角三角形來計算。

把不規則圖形轉化成可以計算面積的規則圖形時,最基本的方法就是割與補,方法不是唯一的,可根據題的特點靈活選擇解法。
上面是坐標系下圖形面積的基本計算方法,實際題目會結合函數來出題,例如我們學過的一次函數。如果有動點,可以化動為靜,然后按照上面的基本方法把圖形面積表示出來。
歡迎使用手機、平板等移動設備訪問中考網,2024中考一路陪伴同行!>>點擊查看