【例題】

如圖①，在四邊形ABCD中，AC⊥BD于點E，AB=AC=BD，點M為BC中點，N為線段AM上的點，且MB=MN

(1)求證：BN平分∠ABE;

(2)若BD=1，連接DN，當四邊形DNBC為平行四邊形時，求線段BC的長;

(3)若點F為AB的中點，連接FN、FM(如圖②)，求證：∠MFN=∠BDC.

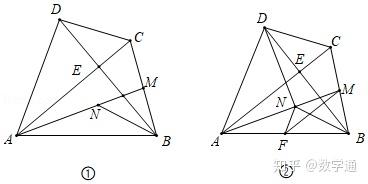
【考查知識點】四邊形綜合題;幾何綜合題

【解題分析】

(1)由AB=AC知∠ABC=∠ACB，由等腰三角形三線合一知AM⊥BC，從而根據(jù)∠MAB+∠ABC=∠EBC+∠ACB知∠MAB=∠EBC，再由△MBN為等腰直角三角形知∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°就可以證明;

(2)設BM=CM=MN=a，知DN=BC=2a，證△ABN≌△DBN得AN=DN=2a，Rt△ABM中利用勾股定理可得a的值，從中得出答案;

(3)F是AB的中點知MF=AF=BF及∠FMN=∠MAB=∠CBD，再由MF/AB=MN/BC=1/2，即MF/BD=MN/BC，得△MFN∽△BDC，即可得證.

【詳細解答】

(1)證明：如圖①，∵AB=AC，

∴∠ABC=∠ACB，

∵M是BC的中點，

∴AM⊥BC，

在Rt△ABM中，∠MAB+∠ABC=90°，

在Rt△CBE中，∠EBC+∠ACB=90°，

∴∠MAB=∠EBC，

∵MB=MN，

∴△MBN是等腰直角三角形，

∴∠MNB=∠MBN=45°，

∵∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°，

∴∠NBE=∠ABN，即BN平分∠ABE;

(2)解：設BM=CM=MN=a，

∵四邊形DNBC是平行四邊形，

∴DN=BC=2a，

在△ABN和△DBN中，

∵AB=DB,角NBE=角ABN，BN=BN

∴△ABN≌△DBN(SAS)，

∴AN=DN=2a，

在Rt△ABM中，由AM2+MB2=AB2，可得：(2a+a)2+a2=1，

解得：a=±根號10/10(負值舍去)，

∴BC=2a=根號10/5;

(3)解：∵F是AB的中點，

∴在Rt△MAB中，MF=AF=BF，

∴∠MAB=∠FMN，

∵∠MAB=∠CBD，

∴∠FMN=∠CBD，

∵MF/AB=MN/BC=1/2，即MF/BD=MN/BC，

∴△MFN∽△BDC，

∴∠MFN=∠BDC.

【總結】

這道題屬于四邊形的綜合題，解決這道題目的關鍵是掌握等腰三角形三線合一的性質、直角三角形和平行四邊形的性質及全等三角形與相似三角形的判定與性質等知識點，如果掌握這些知識點，那么解決起來就不難了。

　　 歡迎使用手機、平板等移動設備訪問中考網，2024中考一路陪伴同行！>>點擊查看