初級的三角函數。是銳角三角函數。他們以銳角為自變量。以比值為函數值。下面我們可以利用平面直角坐標系研究任意角的三角函數。如圖，4-10。設α是一個任意角。二法的終邊上任意一點p。(除端點外)。坐標是(x,y)。它與原點的距離是r(r=√|x|²+|y|²=√x²+y²>0

1:比值y÷r叫做α的正弦。記作sinα

Sinα=y/r

比值x/r叫做α的余弦，記作cosα

Cosα=x/r

比值y/x叫做x的正切，記作tanα

Tanα=y/x

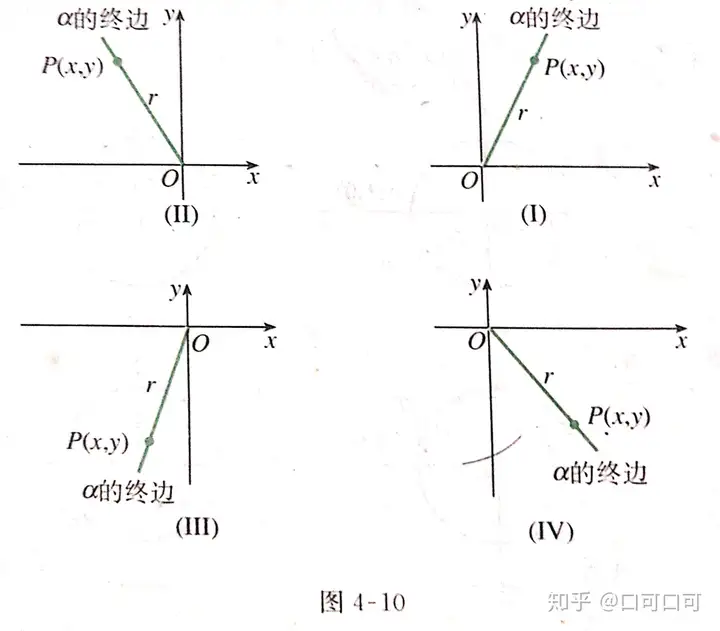
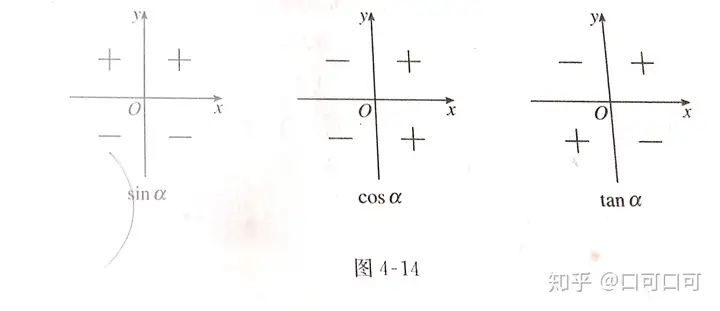
根據相似三角形的知識，對于確定的角α。這三個比值。(如果有的話)都不會隨點p在α的終邊上的位置的改變而改變。

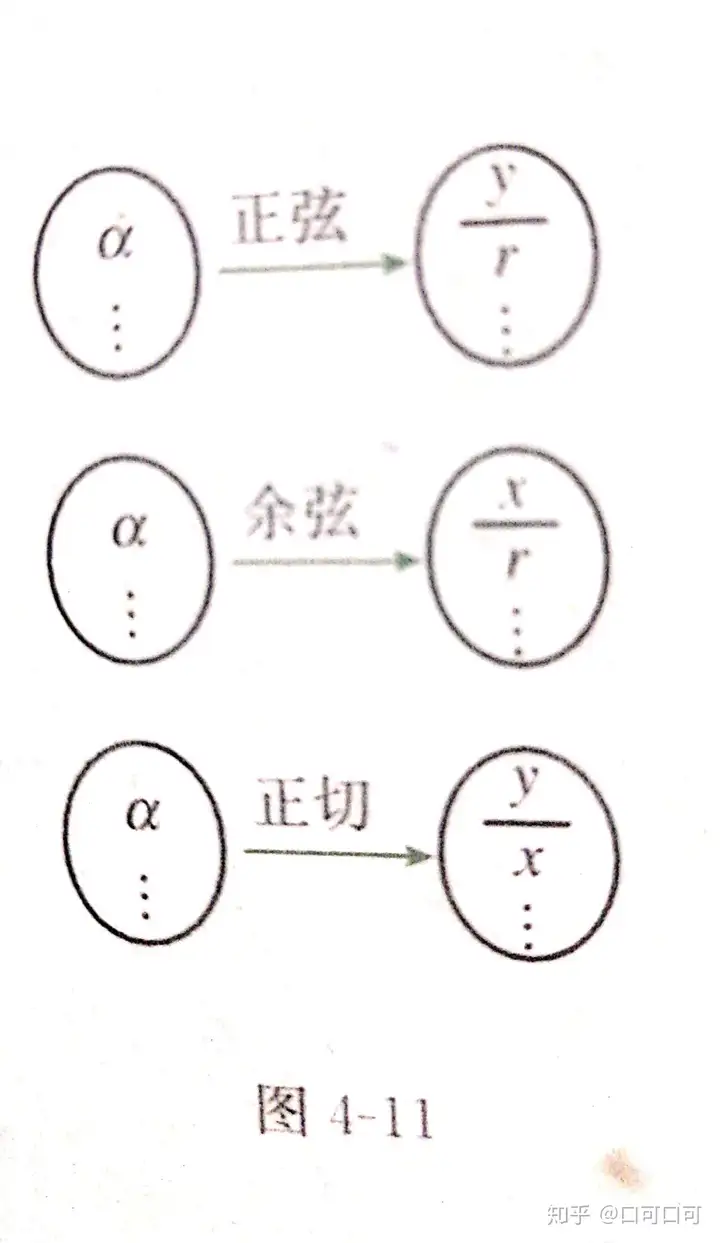
當α=π/2+kπ(k∈Z)時，α的終邊在y軸上終邊上任意一點P的橫坐標都等于0,所以tanα=y/x無意義，除此之外，對于確定的角α,上面的三個比值都是唯一確定的這就是說，正弦，余弦，正切都是以角為自變量，以比值為函數值的函數。圖4-11。來看看正弦，余弦正切這三種三角函數的一種幾何表示。

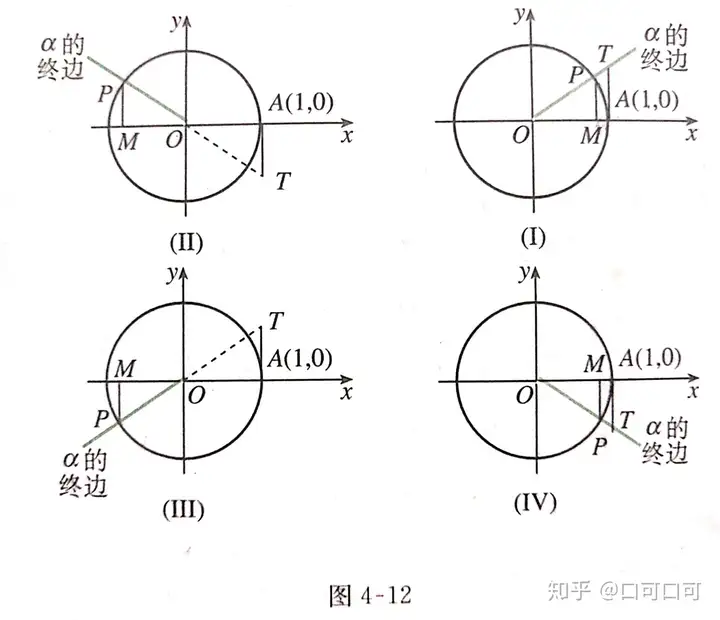
如圖4-12

設任意角α的頂點在原點O,始邊與x軸的非負半軸重合，終邊與單位圓，(圓心在原點O),半徑等于單位長度的圓)相交于點P(x,y),經P作x軸的垂線，垂足為M,過點A(1,0)作單位圓的切線，這條切線必然平行于y軸。設他與角α的終邊(當α為第一四象限角時)或其反向延長線。(當α為第二三象限角時)相交于點T

顯然，線段om的長度為|x|，線段mp的長度。|y|

他們都只能取非負值。

當角阿爾法的終邊不在坐標軸上時，我們可以把om mp都看作帶有方向的線段。

如果x>0把Om看做與x同向，規定，此時om具有正值x。如果x小于零，把om看作`與x軸反向。規定，此時om具有負值x。在這種規定下，不論哪一種情況都有om等于x,如果y大于零，把mp看作與y軸同向。規定此時mp具有正直vi。規定此時mp具有正值y如果y小于零，把mp看作于y軸反向。規定此時mp具有負值y。在這種規定下，不論哪一種情況都有mp等于y.

于是這種對抗中帶有方向的線段叫做有向線段。根據正弦余弦函數的定義就有。

Sinα=y/r=y/1=y=MP,

Cosα=x/r=x/1=x=OM

這兩條與單位圓有關的有向線段mp om分別叫做角阿爾法的正弦線余弦線。

類似的我們也可以把OA,AT看作有向線段那么根據正切函數的定義和相似三角形的知識就有。tanα=y/x=MP/OM=AT

這條與單位圓有關的有向線段AT叫做角α的正切線。

當角阿爾法的終邊在x軸上時，正弦線正切線分別變成一個點。當角阿爾法的終邊在y軸上時，余弦線變成一個點正切線不存在

現在我們分別把表示正切余弦正弦的三個比。y/x,x/r,y/r的前項后項交換，我們又得到三個比。其中。比值x/y叫做α的余切，記作cotα,

比值r/x叫做正割，記作secα,

比值r/y叫做α的余割，記作cscα,

可以看出當α=kπ(k∈Z)時，α的終邊在x軸上，終邊上任意一點P的縱坐標y都等于0，所以cotα=x/y與cscα=r/y的值都不存在，當α=π/2+kπ(k∈Z)時，與與tanα無意義一樣，secα=r/x的值都不存在，除此之外對子確定的角α，比值x/y,r/x,r/y分別是一個確定的實數，所以余切，正割，余割也是以角為自變量。以比值為函數值的函數。以上六種函數統稱三角函數。

由于角的集合與實數集之間可以建立一一對應關系。三角函數可以看成是以實數為自變量的函數。在弧度制下，正弦余弦正切函數的定義域如下表所示。

三角函數

三角函數。

定義域

sinα

R

Cosα

R

Tanα

{α|α≠π/2+kπ,k∈Z｝

由三角函數的定義。以及各象限內點的坐標的符號，我們可以得知。不

正弦值。y/r對于第一二象限角是正的。(y>0,r>0),對于第三四象限角是負的。y<0,r>0

余弦值。x/r對于第一四象限角是正的。(x>0,r>0),對于第二三象限角是負的。(x<0,r>0)

正切值，y/x對于第一，三象限角是正的xy同號。對于第二四象限角是負的x y異號。

三角函數的定義你還可以知道。終邊相同的角的同一三角函數的值相等，由此得到一組公式。

Sin(α+k*360°)=sinα

Cos(α+k*360°)=cosα

Tan(α+k*360°)=tanα其中k∈Z

可以把求任意角的三角函數值轉換為0°到360°角的三角函數值。

       編輯推薦：

       2023年中考各科目重點知識匯總

　　 歡迎使用手機、平板等移動設備訪問中考網，2023中考一路陪伴同行！>>點擊查看