初中數學中主要學習了提取公因式法、運用公式法、分組分解法和十字相乘法，唐老師將在中學數學課本的基礎上，對因式分解的方法、技巧和應用作進一步的深度學習與講解，幫助大家掌握因式分解的技巧。

一、提公因式法.：ma+mb+mc=m(a+b+c)

二、運用公式法.

在整式的乘、除中，我們學過若干個乘法公式，現將其反向使用，即為因式分解中常用的公式，例如：

(1)(a+b)(a-b) = a2-b2 ---------a2-b2=(a+b)(a-b);

(2) (a±b)2 = a2±2ab+b2 ——— a2±2ab+b2=(a±b)2;

(3) (a+b)(a2-ab+b2) =a3+b3------ a3+b3=(a+b)(a2-ab+b2);

(4) (a-b)(a2+ab+b2) = a3-b3 ------a3-b3=(a-b)(a2+ab+b2).

下面再補充兩個常用的公式：

(5)a2+b2+c2+2ab+2bc+2ca=(a+b+c)2;

(6)a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca);

三、分組分解法

(一)分組后能直接提公因式

比如，從“整體”看，這個多項式的各項既沒有公因式可提，也不能運用公式分解，但從“局部”看，這個多項式前兩項都含有a，后兩項都含有b，因此可以考慮將前兩項分為一組，后兩項分為一組先分解，然后再考慮兩組之間的聯系。

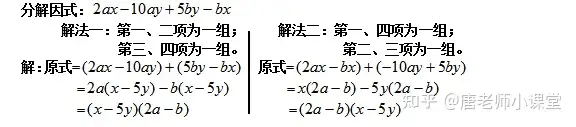
(二)分組后能直接運用公式

分組后能直接運用公式，主要是通過對題目當中各因式的觀察，進行分組后，能夠進行提公因式分解，直到分解的最后能夠變成幾個多項式或單項式與多項式的乘積為止。

綜合練習：

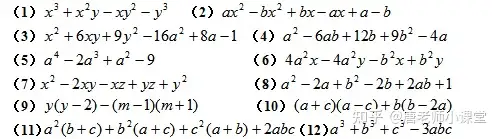
四、十字相乘法.

十字相乘法是因式分解當中比較難的一種分解方式。在運用過程當中，對同學們的思維提出了更高的要求，等大家都熟練了這種方法以后，其實對于因式分解是非常簡單的，而且比較方便。

對于十字相乘法，我們分為四種類型。給大家做詳細的講解。針對每一種方法都有經典的例題解析，通過例題解析的方式讓大家明白因式分解時該如何操作，遵循怎樣的分解步驟，才能比較順利的解決和掌握十字相乘法。

(一)二次項系數為1的二次三項式

直接利用公式——進行分解。

特點：(1)二次項系數是1;

(2)常數項是兩個數的乘積;

(3)一次項系數是常數項的兩因數的和。

(二)二次項系數不為1的二次三項式

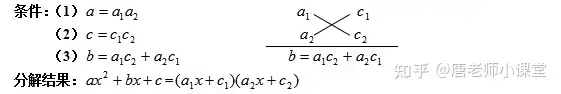
(三)二次項系數為1的齊次多項式

(四)二次項系數不為1的齊次多項式

五、換元法。

換元法在因式分解當中，其難度較大，主要是根據因式分解的要求，對于公因式當中出現了比較大的數字或多項式時，同學們很難在短時間內看到十字相乘法的簡單形式，所以通過換元的方式，把相同的多項式或數字用簡單的字母來代替，這樣對于用十字相乘法時更加的明顯，也比較簡單，最后再將換元的形式補充回來，就可以得到最后因式分解的形式，這種方法在解題時能極大的提高同學們的解題效率，而且從形式上會使原來的式子變得更加的簡單。

六、添項、拆項、配方法。

天象拆項配方法是在以上幾種方法進行因式分解未果的情況下才考慮的因式分解的另一種形式。這種分配的方式其難度以及要求的思維能力比起前面的幾種方式都比較高。學習這幾種方法，一定在平時就要加強訓練，把這種方法靈活運用能力提高到新的高度，否則當真正遇到這類題型時，很難快速的得到解決的方案，以至于降低了學習效率。

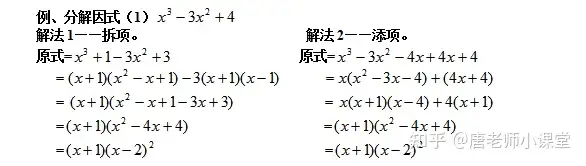
七、待定系數法。

待定系數法在因式分解的方法當中算是獨一份。主要采用逆向思維的方法，從猜想到的結論當中進行。解方程的形式來得到因式分解的結果，這種方法對于提升同學們的數學思維有比較好的促進作用，建議想要提升數學思維的同學，進行加強練習。

在一般的分解因式當中，這種方法能用到的頻率并不高，但是對于有關因式分解中求參數的知識運用比較廣泛，具體的方法，我們通過經典的例題解析來給大家一一呈現。

　　 歡迎使用手機、平板等移動設備訪問中考網，2024中考一路陪伴同行！>>點擊查看