三角形常見輔助線

1.在利用三角形三邊關系證明線段不等關系時，如果直接證不出來，可連結兩點或延長某邊構造三角形，使結論中出現的線段在一個或幾個三角形中，再利用三邊關系定理及不等式性質證題.

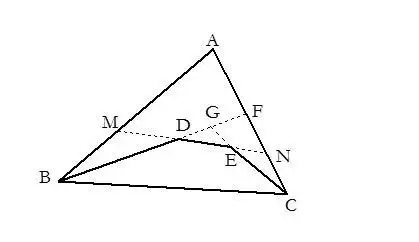
注意：利用三角形三邊關系定理及推論證題時，常通過引輔助線，把求證的量(或與求證有關的量)移到同一個或幾個三角形中去然后再證題.

2.在利用三角形的外角大于任何和它不相鄰的內角證明角的不等關系時，如果直接證不出來，可連結兩點或延長某邊，構造三角形，使求證的大角在某個三角形外角的位置上，小角處在內角的位置上，再利用外角定理證題.

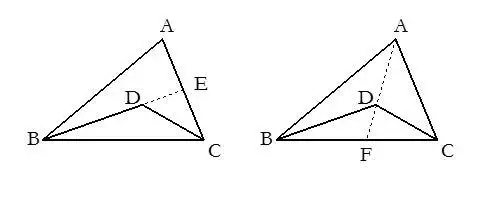
3.有角平分線時常在角兩邊截取相等的線段，構造全等三角形.

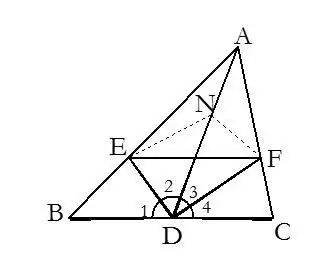
4. 有以線段中點為端點的線段時，常加倍延長此線段構造全等三角形.

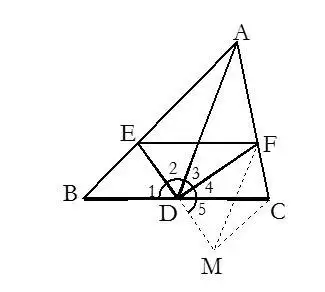
5.在三角形中有中線時，常加倍延長中線構造全等三角形.

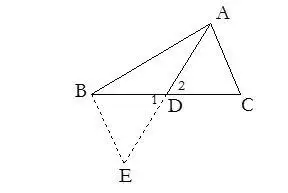
6.截長補短作輔助線的方法

截長法：在較長的線段上截取一條線段等于較短線段;

補短法：延長較短線段和較長線段相等.

這兩種方法統稱截長補短法.

當已知或求證中涉及到線段a、b、c、d有下列情況之一時用此種方法：

①a>b

②a±b = c

③a±b = c±d

7.證明兩條線段相等的步驟：

①觀察要證線段在哪兩個可能全等的三角形中，然后證這兩個三角形全等。

②若圖中沒有全等三角形，可以把求證線段用和它相等的線段代換，再證它們所在的三角形全等.

③如果沒有相等的線段代換，可設法作輔助線構造全等三角形.

8.在一個圖形中，有多個垂直關系時，常用同角(等角)的余角相等來證明兩個角相等.

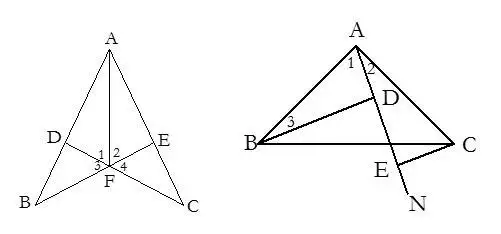
9.三角形一邊的兩端點到這邊的中線所在的直線的距離相等.

10.條件不足時延長已知邊構造三角形.

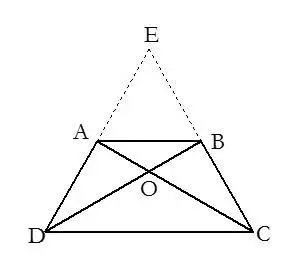
11.連接四邊形的對角線，把四邊形問題轉化成三角形來解決問題.

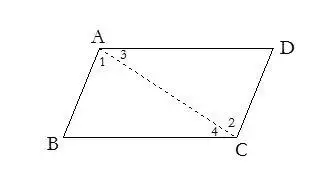
12.有和角平分線垂直的線段時，通常把這條線段延長。可歸結為“角分垂等腰歸”

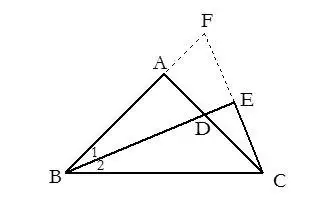
13.當證題有困難時，可結合已知條件，把圖形中的某兩點連接起來構造全等三角形。

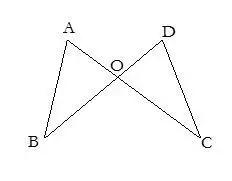
14.當證題缺少線段相等的條件時，可取某條線段中點，為證題提供條件.

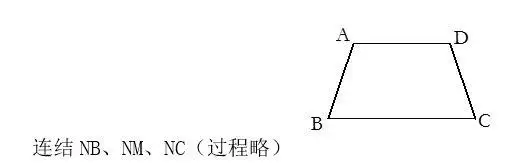
例：已知，如圖，AB = DC，∠A = ∠D

求證：∠ABC = ∠DCB

證明：分別取AD、BC中點N、M，

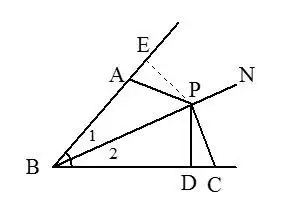
15.有角平分線時，常過角平分線上的點向角兩邊做垂線，利用角平分線上的點到角兩邊距離相等證題.

18.有垂直平分線時常把垂直平分線上的點與線段兩端點連結起來.

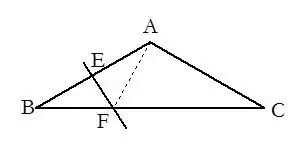
19.有垂直時常構造垂直平分線.

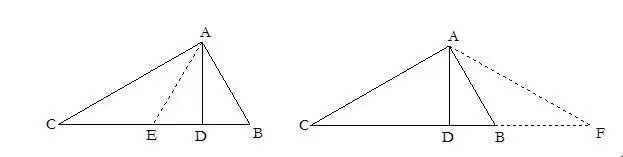
20.有中點時常構造垂直平分線.

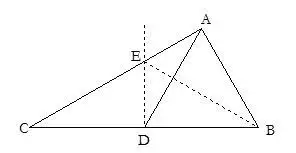
21.當涉及到線段平方的關系式時常構造直角三角形，利用勾股定理證題.

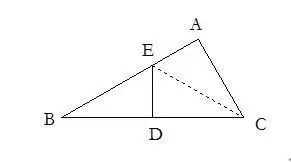
22.條件中出現特殊角時常作高把特殊角放在直角三角形中.

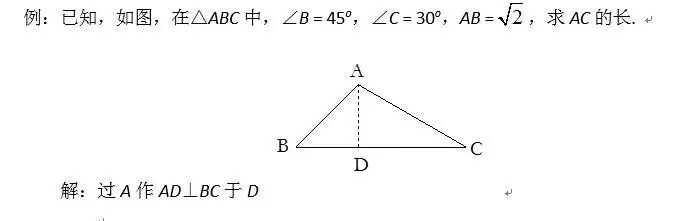
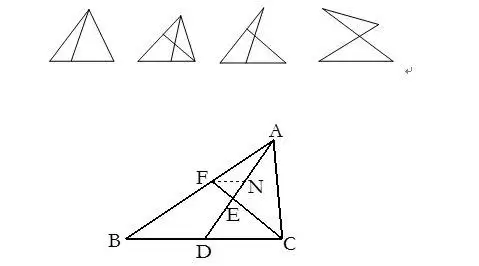
23.當圖形中有叉線(基本圖形如下)時，常作平行線.

　　 歡迎使用手機、平板等移動設備訪問中考網，2024中考一路陪伴同行！>>點擊查看