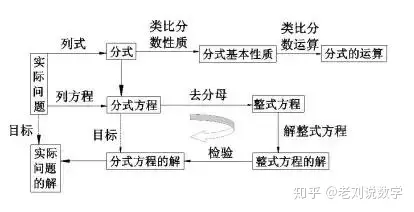
從代數與運算→方程與解析，從數與式→式與方程→方程與應用→方程與函數解析的關系，我們可以看出這是初中代數部分的一個整體思維和學習脈絡。現在我們來鞏固下有關分式的相關知識。

基礎知識點

1、分式：

(1)分式的定義：如果A、B表示兩個整式，并且B中含有字母，那么式子A/B叫做分式。

(2)分式是否有意義的條件：分式的分母是否等于0，有意義則分母不為0，無意義則分母為0。

(3)分式值為零的條件：分式A/B=0的條件是A=0，且B≠0。

注意：求出使分子為0的字母的值，一定要注意檢驗這個字母的值是否使分母的值為0，一般當分母的值不為0時，就是所要求的字母的值。

(4)分式的基本性質：分式的分子與分母同乘(或除以)一個不等于0的整式，分式的值不變。

(5)分式的通分：利用分式的基本性質，使分子和分母同乘適當的整式，不改變分式的值，把幾個異分母分式化成相同分母的分式，這樣的分式變形叫做分式的通分。

注意：通分的關鍵是確定幾個式子的最簡公分母。幾個分式通分時，通常取各分母所有因式的最高次冪的積作為公分母，這樣的分母就叫做最簡公分母。求最簡公分母時應注意以下幾點：

● “各分母所有因式的最高次冪”是指凡出現的字母(或含字母的式子)為底數的冪選取指數最大的;

● 如果各分母的系數都是整數時，取它們系數的最小公倍數作為最簡公分母的系數;

● 如果分母是多項式，一般應先分解因式。

(6)分式的約分：根據分式的基本性質，約去分式的分子和分母中的公因式，不改變分式的值，這樣的分式變形叫做分式的約分。

約分后分式的分子、分母中不再含有公因式，這樣的分式叫最簡公因式。

注意：約分的關鍵是找出分式中分子和分母的公因式

◆(1)約分時注意分式的分子、分母都是乘積形式才能進行約分;分子、分母是多項式時，通常將分子、分母分解因式，然后再約分;

◆(2)找公因式的方法：

① 當分子、分母都是單項式時，先找分子、分母系數的最大公約數，再找相同字母的最低次冪，它們的積就是公因式;

②當分子、分母都是多項式時，先把多項式因式分解。

　　 歡迎使用手機、平板等移動設備訪問中考網，2024中考一路陪伴同行！>>點擊查看