Ž┬├µ╬ęéāŽ╚üĒ┐┤┐┤Ę┤▒╚└²║»öĄĄ─æ¬ė├Č╝ėą──ą®ųžę¬Ą─Ą─║╦ą─ų¬ūR³c?
1.└¹ė├┤²Č©ŽĄöĄĘ©┤_Č©Ę┤▒╚└²║»öĄĮŌ╬÷╩Į
ė╔ė┌Ę┤▒╚└²║»öĄy=k/xųąų╗ėąę╗éĆ┤²Č©ŽĄöĄ��Ż¼ę“┤╦ų╗ę¬ę╗ī”ī”æ¬Ą─x�����Ż¼yųĄŻ¼╗“ęčų¬ŲõłDŽ±╔Žę╗éĆ______Ą─ū°ś╦╝┤┐╔Ū¾│÷k��Ż¼▀MČ°┤_Č©Ę┤▒╚└²║»öĄĄ─ĮŌ╬÷╩Į.
2.Ę┤▒╚└²║»öĄĄ─īŹļHæ¬ė├
ĮŌøQĘ┤▒╚└²║»öĄæ¬ė├å¢Ņ}Ģr�Ż¼╩ūŽ╚꬚ę│÷┤µį┌Ę┤▒╚└²ĻPŽĄĄ─ā╔éĆūā┴┐Ż¼╚╗║¾Į©┴óĘ┤▒╚└²║»öĄ─Żą═���Ż¼▀MČ°└¹ė├Ę┤▒╚└²║»öĄĄ─ėąĻPų¬ūR╝ėęįĮŌøQ.
3.Ę┤▒╚└²║»öĄKĄ─Äū║╬ęŌ┴x
4.Ę┤▒╚└²║»öĄ┼cłDą╬├µĘeå¢Ņ}
|
┐╝ŠVę¬Ū¾ |
├³Ņ}┌ģä▌ |
|
1Ż«└¹ė├┤²Č©ŽĄöĄĘ©┤_Č©Ę┤▒╚└²║»öĄĮŌ╬÷╩Į2Ż«Ę┤▒╚└²║»öĄ┼cłDą╬Ą─├µĘeå¢Ņ}Ż«3Ż«─▄ė├Ę┤▒╚└²║»öĄĮŌøQ║åå╬īŹļHå¢Ņ}. |
Ę┤▒╚└²║»öĄĄ─æ¬ė├╩Ūųą┐╝├³Ņ}¤ß³cų«ę╗Ż¼���Ż¼Įø│Ż┼cę╗┤╬║»öĄĪóČ■┤╬║»öĄ╝░Äū║╬łDą╬Ą╚ų¬ūRŠC║Ž┐╝▓ķŻ«┐╝▓ķą╬╩Įęį▀xō±Ņ}��Īó╠Ņ┐šŅ}×ķų„��Ż¼ęį╝░┼cę╗┤╬║»öĄĄ─ŠC║ŽŅ}. |
Ųõ┤╬��Ż¼ŠoĖ·┐╝³cĄ─ĘųŅÉŻ¼šŲ╬šĮŌŅ}Ą─ĘĮĘ©║═ĮŌŅ}Ą─ŲŲŅ}³c���ĪŻ
┐╝³cę╗��ĪóĘ┤▒╚└²║»öĄĮŌ╬÷╩ĮĄ─┤_Č©
ĪŠ└²1Ī┐╚ńłD����Ż¼ų▒ŠĆy=2x┼cĘ┤▒╚└²║»öĄy=k/xĄ─łDŽ±į┌Ą┌ę╗Ž¾Ž▐Ą─Į╗³c×ķA�����Ż¼AB┤╣ų▒ė┌x▌S����Ż¼┤╣ūŃ×ķB���Ż¼ęčų¬OB=1���Ż¼Ū¾³cAĄ─ū°ś╦║═▀@éĆĘ┤▒╚└²║»öĄĄ─ĮŌ╬÷╩Į.
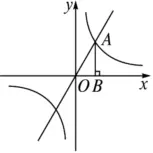
ĪŠĘĮĘ©┐éĮYĪ┐Ę┤▒╚└²║»öĄų╗ėąę╗éĆ╗∙▒Š┴┐k��Ż¼╣╩ų╗ąĶę╗éĆŚl╝■╝┤┐╔┤_Č©Ę┤▒╚└²║»öĄ.▀@éĆŚl╝■┐╔ęį╩ŪłDŽ±╔Žę╗³cĄ─ū°ś╦��Ż¼ę▓┐╔ęį╩Ūx�Ż¼yĄ─ę╗ī”ī”æ¬ųĄ.
┐╝³cČ■��ĪóĘ┤▒╚└²║»öĄīŹļHæ¬ė├
ĪŠ└²2Ī┐ęčų¬ę╗╦ę▌å┤¼╔Žčbėą100揞ø╬’����Ż¼▌å┤¼ĄĮ▀_─┐Ą─Ąž║¾ķ_╩╝ąČžø.įOŲĮŠ∙ąČžø╦┘Č╚×ķv(å╬╬╗Ż║ćŹ/ąĪĢr)�Ż¼ąČ═Ļ▀@┼·žø╬’╦∙ąĶĄ─Ģrķg×ķt(å╬╬╗Ż║ąĪĢr).
(1)Ū¾vĻPė┌tĄ─║»öĄ▒Ē▀_╩Į.
(2)╚¶ę¬Ū¾▓╗│¼▀^5ąĪĢrąČ═Ļ┤¼╔ŽĄ─▀@┼·žø╬’Ż¼─Ū├┤ŲĮŠ∙├┐ąĪĢrų┴╔┘ꬹȞøČÓ╔┘ćŹ?

┐╝³c╚²�����ĪóĘ┤▒╚└²║»öĄĄ─▒╚└²ŽĄöĄkĄ─Äū║╬ęŌ┴x
ĪŠ└²3Ī┐ęčų¬³cPį┌║»öĄy=2/x(x>0)Ą─łDŽ¾╔Ž�Ż¼PA⊥x▌S���Ż¼PB⊥y▌S���Ż¼┤╣ūŃĘųäe×ķA�Ż¼BŻ¼ätŠžą╬OAPBĄ─├µĘe×ķ__________.
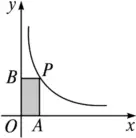
ĪŠĮŌ╬÷Ī┐įOp³cū°ś╦×ķ(x�Ż¼y)�����Ż¼Šžą╬OAPBĄ─├µĘeĄ╚ė┌|xy|=|k|=2.
ĪŠĘĮĘ©┐éĮYĪ┐▀^ļpŪ·ŠĆ╔Ž╚╬ęŌę╗³cū÷x▌SĪóy▌SĄ─┤╣ŠĆŻ¼╦∙Ą├Šžą╬Ą─├µĘe×ķ|k|;▀^ļpŪ·ŠĆ╔Ž╚╬ęŌę╗³c┼cįŁ³c╦∙▀BĄ─ŠĆČ╬���Īóū°ś╦▌SĪóŽ“ū°ś╦▌Sū„┤╣ŠĆ╦∙ć·│╔Ą─ų▒ĮŪ╚²ĮŪą╬Ą─├µĘeS=1/2|k|.
┐╝³c╦─ĪóĘ┤▒╚└²║»öĄ┼cłDą╬├µĘeå¢Ņ}
ĪŠ└²4Ī┐╚ńłDŻ¼─│Ę┤▒╚└²║»öĄłDŽ±Ą─ę╗ų¦Įø▀^³cA(2Ż¼3)║═³cB(³cBį┌³cAĄ─ėęé╚)����Ż¼ū„BC⊥y▌S�����Ż¼┤╣ūŃ×ķ³cCŻ¼▀BĮYABŻ¼AC.
(1)Ū¾įōĘ┤▒╚└²║»öĄĄ─ĮŌ╬÷╩Į;
(2)╚¶Ī„ABCĄ─├µĘe×ķ6���Ż¼Ū¾ų▒ŠĆABĄ─▒Ē▀_╩Į.
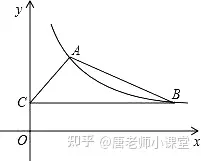

ĪŠĘĮĘ©┐éĮYĪ┐╠Ä└ĒĘ┤▒╚└²║»öĄųąłDą╬Ą─├µĘeå¢Ņ}Ż¼╩ūŽ╚ę¬įO│÷╬┤ų¬³cĄ─ū°ś╦Ż¼╚╗║¾▒Ē╩Š│÷╚²ĮŪą╬╗“š▀╦─▀ģą╬Ą─├µĘeŻ¼ĮĶų·ė┌ŲĮ├µų▒ĮŪū°ś╦ŽĄųąĄ─ę╗┤╬║»öĄ╗“š▀Ę┤▒╚└²║»öĄĄ─ĮŌ╬÷╩Į▀Mąą▒Ē╩Šū°ś╦��ĪŻĻPµIę¬ūźūĪŪĪ«öĄ─ķLČ╚ū„×ķĄū║═Ė▀�����ĪŻ
ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC����ĪóŲĮ░ÕĄ╚ęŲäėįOéõįLå¢ųą┐╝ŠW����Ż¼2024ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą���ŻĪ>>³cō¶▓ķ┐┤














