特殊值法是我們在做選擇題和填空題時最常用的快捷方法之一，今天這道求反比例函數表達式題，就可以使用該方法迅速得到答案，照例，我們先看題目和常規解法：

如圖，等腰直角三角形的兩個銳角頂點A、B分別在x軸、y軸上，直角頂點P在反比例函數不等式組y=kx(k≠0)的圖象上，若OA+OB=23，則k的值為________。

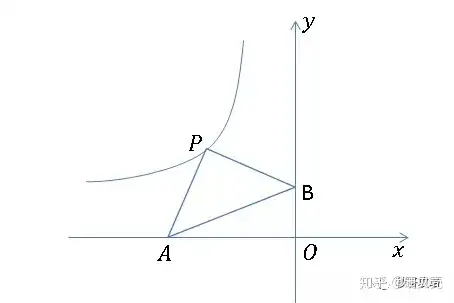
[常規思路解析]

1. 要求k的值，其實就是求雙曲線上的點的橫縱坐標的乘積，本題中只給出來貌似與雙曲線不太相關的OA和OB的和，似乎無從下手。

2. 既然沒有可以直接得到答案的思路，我們就只有反推了。設雙曲線上的P點坐標為(x, y)，我們來看x、y與OA和OB有何關系。

3. 做輔助線如下：

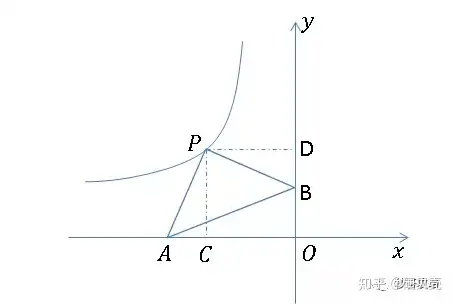
PC即為y，PD為-x，由題目所給條件，ΔABP為等腰直角三角形易證ΔPAC≌ΔPBD，且PCOD為正方形，PC+PD=OD+OC=OB+OA。

4. 然后，就可以不用然后了^_^

[解答]

此題給我們的提示是：要求反比例函數(雙曲線)表達式，一般來說要找到雙曲線上一點，向兩個坐標軸做垂線段，然后利用幾何法或代數法求解。But... ...對于本題，一道填空題來說，秒答君教您使用特殊值法秒答之。

[解析]

1. 首先仔細觀察題干，找出隱含條件：k值為定值，且與OA、OB的長度無關。

2. 因此，我們取一個特殊位置，當OA=OB=3時，PA=PB=3，此時K=-3。

提示：對于選擇題和填空題要善于挖掘題目給出的隱含條件，并充分利用題目本身的缺陷，使用相應的方法如排除法、極值法、特殊值法等，快速得到答案。

　　 歡迎使用手機、平板等移動設備訪問中考網，2024中考一路陪伴同行！>>點擊查看