全等模型之三垂直、三等角模型

三垂直、三等角模型

定義：三個等角的頂點在同一條直線上構成的圖形，這個角可以是直角，也可以是銳角或鈍角，一般是以等腰三角形或者等邊三角形為背景。這個模型貫穿初中幾何的始終，初三講《相似三角形》時這也是一個非常重要的知識點

方法提煉

1 若題目中有一線三(直角)等角，可以直接證明相似或全等實現邊與角的轉化;

2 若題目中沒有給出一線三(直角)等角，可以根據需要來構造

基本模型：(1)一線三垂直

【基本圖形】

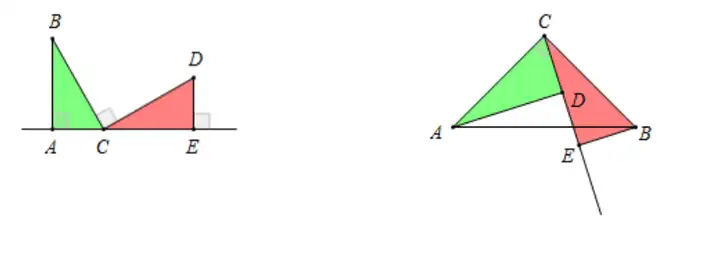
全等模型之半角模型

定義：夾半角，顧名思義，是一個大角夾著一個大小只有其一半的角，如下圖所示。

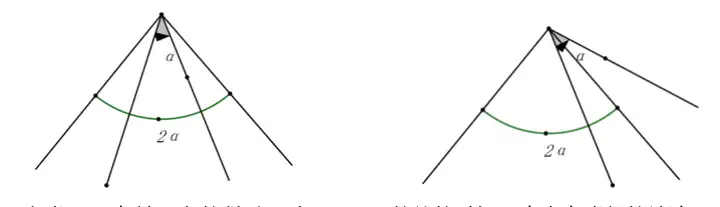
這類題目有其固定的做法，當a取不同的值的時候，也會有類似的結論

夾半角的常見分類：

(1)90 度夾 45 度

(2)120 度夾 60 度

(3)2α夾α

題型一 90 度夾 45 度

【例 1】 如圖，正方形ABCD 中，E在BC上，F在CD上，且∠EAF=45°，求證：(1)BE+DF=EF

(2)∠AEB=∠AEF

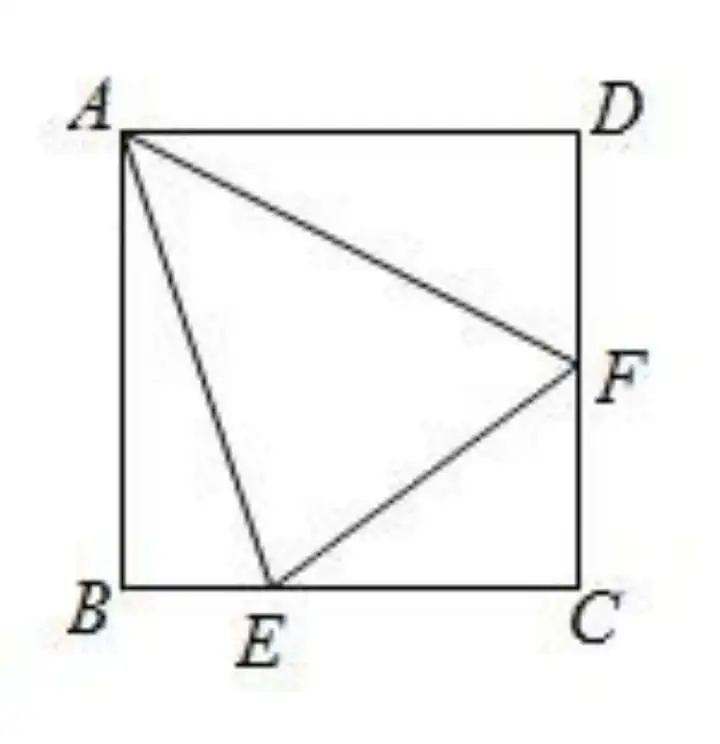
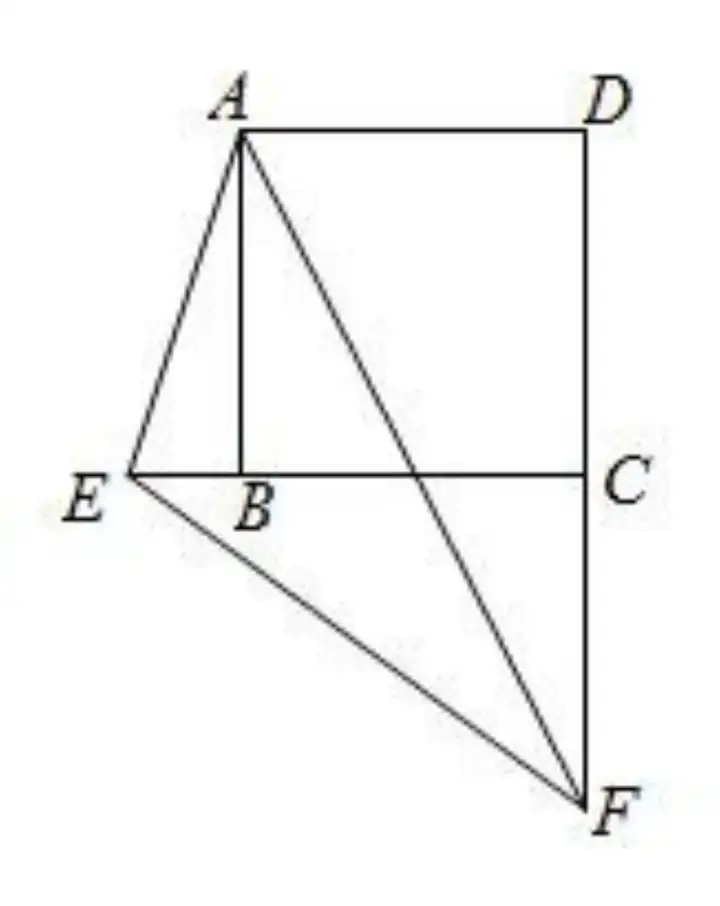
(2)在例 1 的條件下，若E在CB延長線上，F在DC延長線上，其余條件不變，證明：

(1)DF-BE=EF

(2)∠AEB+∠AEF=180°

中點模型

模型1.倍長中線或類中線(與中點有關的線段)構造全等三角形

如圖①，AD是△ABC的中線，延長AD至點E使DE=AD，易證：△ADC≌EDB(SAS)。

如圖②，D是BC中點，延長FD至點E使DE=FD，易證：△FDB≌△EDC(SAS)。

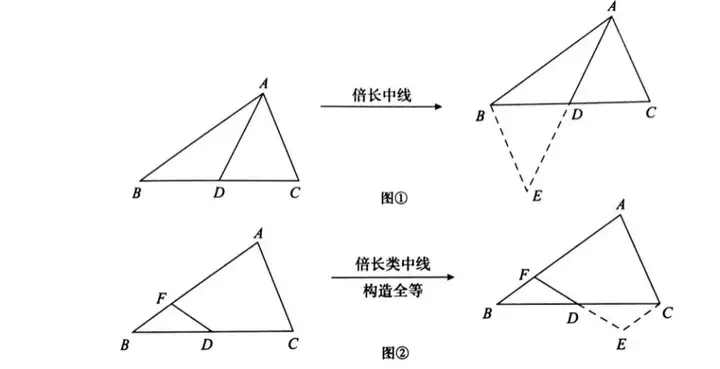
模型分析：

當遇見中線或者中點的時候，可以嘗試倍長中線或倍長類中線，構造全等三角形，目的是對已知條件中的線段進行轉移。

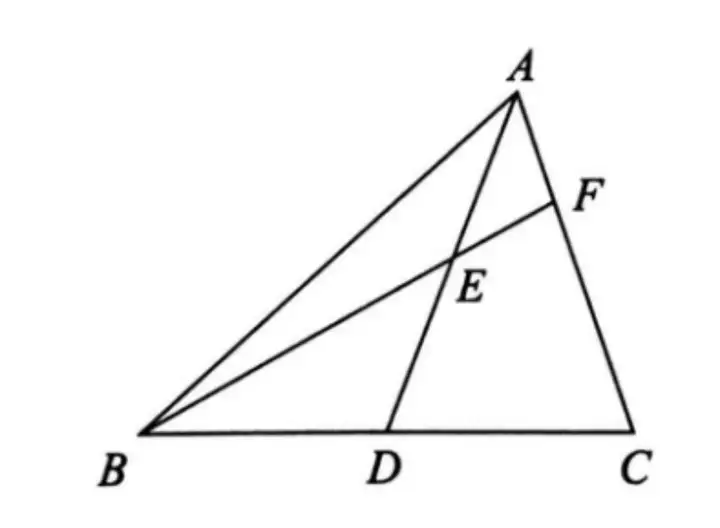
例1. 如圖，已知在△ABC中，AD是BC邊上的中線，E是AD上一點，連接BE并延長交AC于點F，AF=EF。求證：AC=BE。

模型2.已知等腰三角形底邊中點，可以考慮與頂點連接用“三線合一”

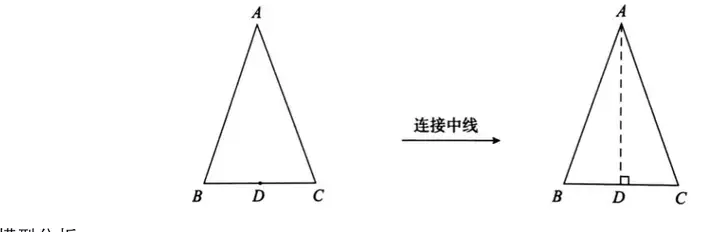
模型分析：

等腰三角形有底邊中點時，常作底邊的中線，利用等腰三角形“三線合一”的性質得到角相等或邊相等。為解題創造更多的條件，當看到等腰三角形的時候，就應想到“邊等、角等、三線合一”。

例.如圖，在△ABC中，AB=AC=5，BC=6，M為BC的中點，MN⊥AC于點N，求MN的長度。

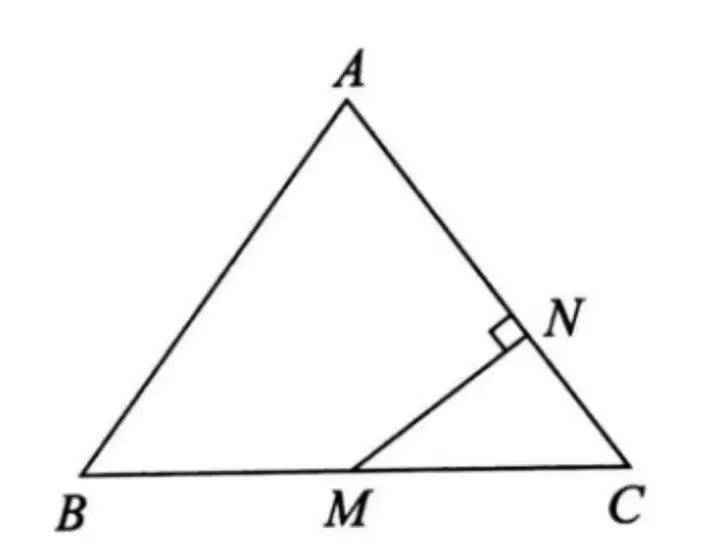
模型3.已知三角形一邊的中點，可以考慮中位線定理

模型分析：

在三角形中，如果有中點，可構造三角形的中位線，利用三角形中位線的性質定理：DE∥BC，且DE=1/2BC來解題。中位線定理中既有線段之間的位置關系又有數量關系，該模型可以解決角相等，線段之間的倍半、相等及平行問題。

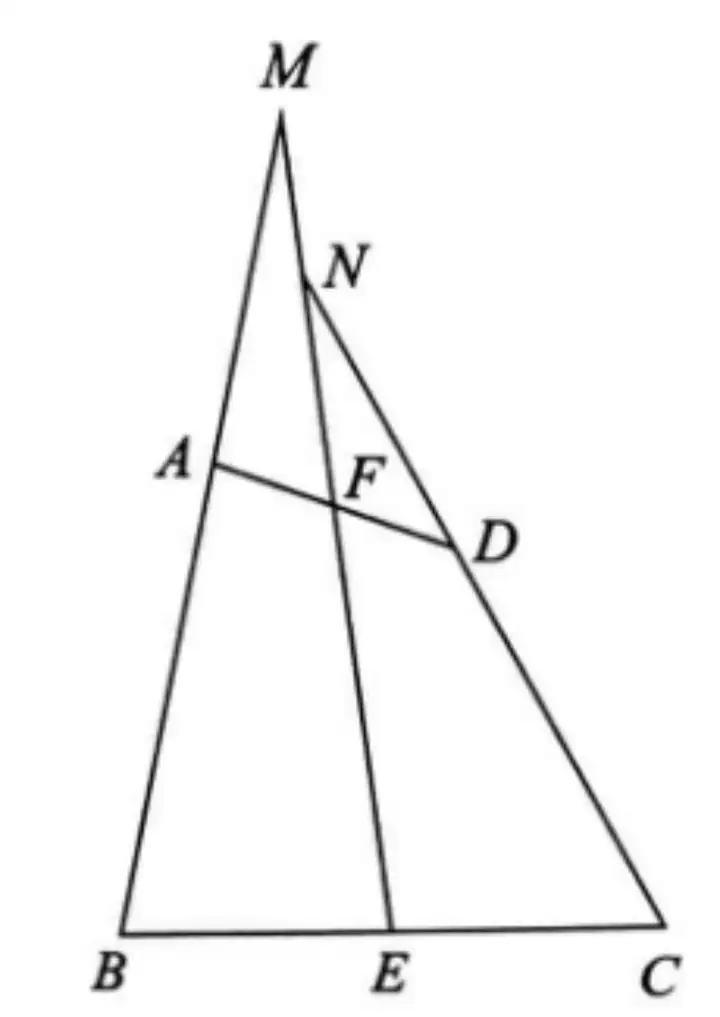
例. 在四邊形ABCD中，AB=CD，E、F分別是BC、AD的中點，連接EF并延長，分別與BA、CD的延長線交于點M、N。求證：∠BME=∠CNE。

模型4.已知直角三角形斜邊中點，可以考慮構造斜邊中線

模型分析：

在直角三角形中，當遇見斜邊中點時，經常會作斜邊上的中線，利用直角三角形斜邊上的中線等于斜邊的一半，即CD=1/2AB，來證明線段間的數量關系，而且可以得到兩個等腰三角形：△ACD和△BCD，該模型經常會與中位線定理一起綜合應用。

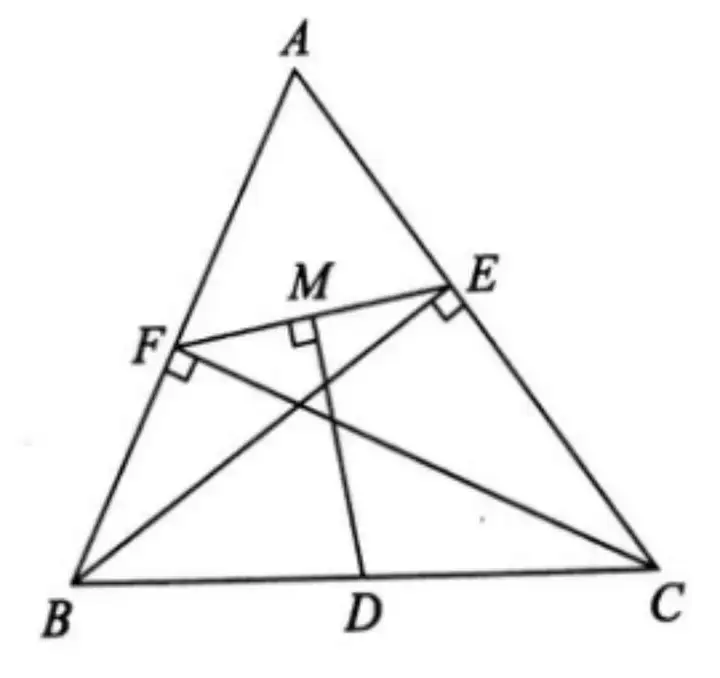
例. 如圖，在△ABC中，BE、CF分別為AC、AB上的高，D為BC的中點，DM⊥EF于點M。求證：FM=EM。

手拉手模型

例1、在直線ABC的同一側作兩個等邊三角形△ABD和△BCE，連接AE與CD，證明：

(1) △ABE≌△DBC

(2) AE=DC

(3) AE與DC的夾角為60。

(4) △AGB≌△DFB

(5) △EGB≌△CFB

(6) BH平分∠AHC

(7) GF∥AC

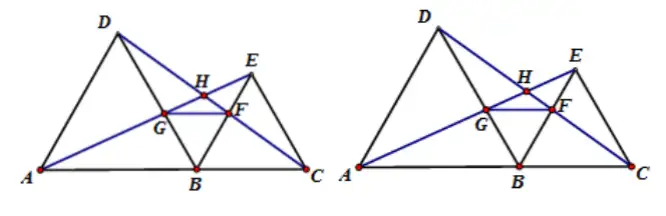
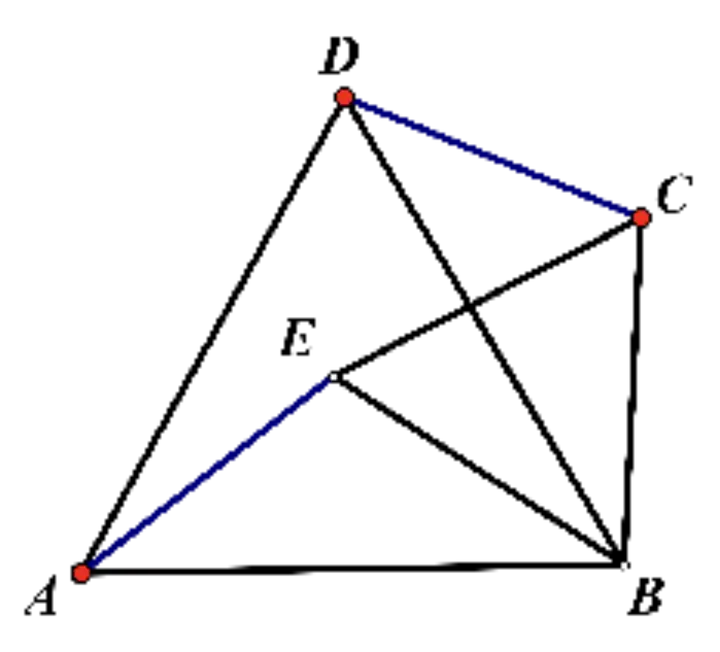
變式練習1、如果兩個等邊三角形△ABD和△BCE，連接AE與CD，證明：

(1) △ABE≌△DBC

(2) AE=DC

(3) AE與DC的夾角為60。

(4) AE與DC的交點設為H,BH平分∠AHC

奔馳模型

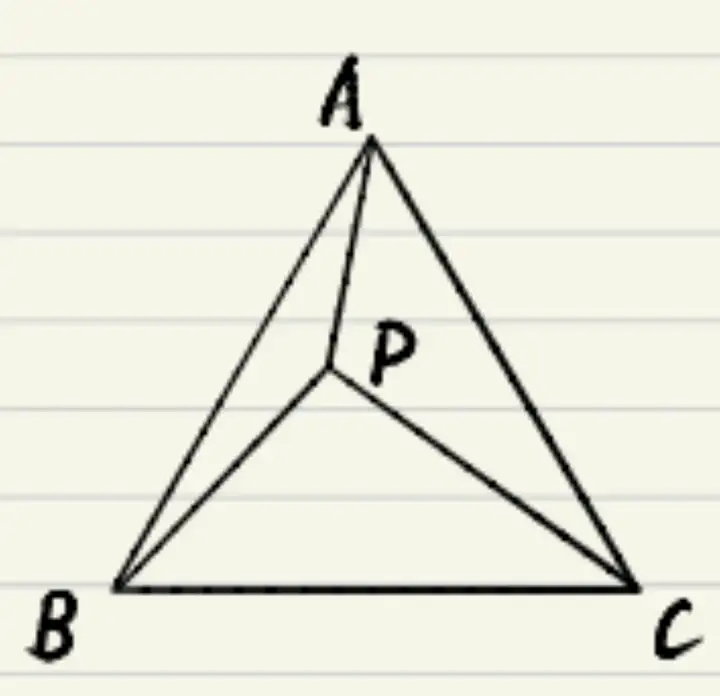
截長補短

截長補短法構造全等三角形

截長補短法，是初中數學幾何題中一種輔助線的添加方法，也是把幾何題化難為易的一種思想.所謂“截長”，就是將三者中最長的那條線段一分為二，使其中的一條線段等于已知的兩條較短線段中的一條，然后證明其中的另一段與已知的另一條線段相等;所謂“補短”，就是將一個已知的較短的線段延長至與另一個已知的較短的長度相等，然后求出延長后的線段與最長的已知線段的關系.有的是采取截長補短后，使之構成某種特定的三角形進行求解.

截長補短法作輔助線，適合于證明線段的和、差、倍、分等類的題目.

　　 歡迎使用手機、平板等移動設備訪問中考網，2023中考一路陪伴同行！>>點擊查看