初三數學——幾何變換

平移、旋轉和翻折是幾何變換中的三種基本變換。所謂幾何變換就是根據確定的法則，對給定的圖形(或其一部分)施行某種位置變化，然后在新的圖形中分析有關圖形之間的關系。

旋轉

一、旋轉的定義

二、常見的幾種模型

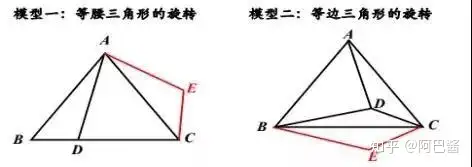
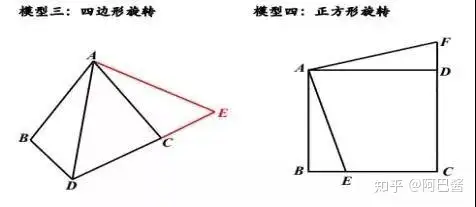
三、旋轉類型題目

1、正三角形類型

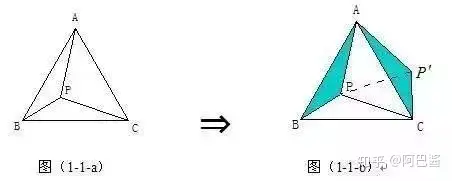
在正ΔABC中，P為ΔABC內一點，將ΔABP繞A點按逆時針方向旋轉60°，使得AB與AC重合。經過這樣旋轉變化，將圖(1-1-a)中的PA、PB、PC三條線段集中于圖(1-1-b)中的一個ΔP'CP中，此時ΔP'AP也為正三角形。

2、正方形類型

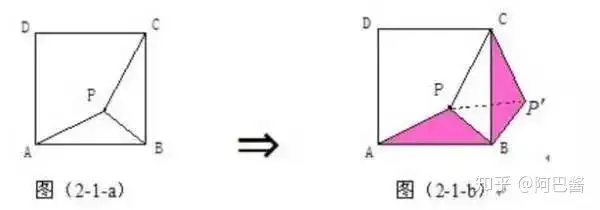
在正方形ABCD中，P為正方形ABCD內一點，將ΔABP繞B點按順時針方向旋轉90°，使得BA與BC重合。經過旋轉變化，將圖(2-1-a)中的PA、PB、PC三條線段集中于圖(2-1-b)中的ΔCPP'中，此時ΔBPP'為等腰直角三角形。

3、等腰直角三角形類型

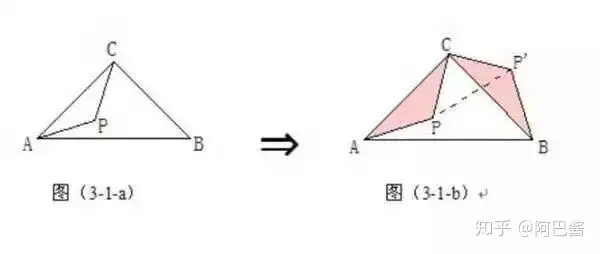
在等腰直角三角形ΔABC中，∠C=90°, P為ΔABC內一點，將ΔAPC繞C點按逆時針方向旋轉90°，使得AC與BC重合。經過這樣旋轉變化，在圖(3-1-b)中的一個ΔP'CP為等腰直角三角形。

平移

1、平移的定義

把一個圖形沿著一定的方向平行移動而達到另一個位置，這種圖形的平行移動簡稱為平移。

2、平移的兩個要素：

(1)平移方向;(2)平移距離。

3、對應點、對應線段、對應角

一個圖形經過平移后得到一個新的圖形，這個新圖形與原圖形是能夠互相重合的全等形，我們把互相重合的點稱為對應點，互相重合的線段稱為對應線段，互相重合的角稱為對應角。

4、平移方向和距離的確定

(1)要對一個圖形進行平移，在平移前必須弄清它的平移方向和平移距離，否則將無法實現平移，那么怎樣確定這兩點呢?

A. 若給出帶箭頭的線段：從箭尾到箭頭的方向表示平移方向，而帶箭頭的線段的長度，表示平移距離，也有時另給平移距離的長度。

B. 若給出由小正方形組成的方格紙：在方格中的平移，從方向上看往往是要求用橫縱兩次平移來完成(有特殊要求例外)，而移動距離是由最終要達到的位置確定的。

C. 具體給出從某點P到另一點P'的方向為平移方向，線段PP'的長度為平移距離。

D. 給出具體方位(如向東或者西北等)和移動長度(如10CM)。

(2)圖形平移后，平移方向與平移距離的確定。

圖形平移后，原圖形與新圖形中的任意一對前后對應點的射線方向就是原平移方向，這對對應點間的線段長度就是原平移距離。

5、平移性質

圖形平移的實質是圖形上的每一點都沿著同一個方向移動了相同的距離。

平移后的圖形與原圖形：

① 對應線段平行(或在同條一直線上)且相等;

② 對應點連線平行(或在同一條直線上)且相等;

③ 圖形的形狀與大小都不變(全等);

④ 圖形的頂點字母的排列順序的方向不變。

6、判別平移圖形：

除根據定義判別外，還可以根據平移特征，從中去掉那些能互相替代和包含的內容，只要具備以下三條：

(1)這兩個圖形必須是全等形;

(2)這兩個全等形的對應線段必須互相平行(或者在同一條直線上);

(3)這兩個全等形的對應點連線必須互相平行(或在同一條直線上)。

以上為判別方法一，由判別方法一還可以演變推出如下判別方法二:

(1)這兩個圖形必須是全等形;

(2)這兩個全等形的對應頂點字母的排列順序在圖中的方向必須相同(同位順時針或同為逆時針);

(3)這兩個全等形的對應點連線必須互相平行(或在同一條直線上)。

翻折

一、翻折的定義

翻折和折疊問題其實質就是對稱問題，翻折圖形的性質就是翻折前后圖形是全等的，對應的邊和角都是相等的。以這個性質為基礎，結合圓的性質，三角形相似，勾股定理設方程思想來考查。

二、翻折的性質

①翻折后兩個圖形全等，對應邊相等，對應角相等。

②對應點連線被對稱軸垂直平分。

三、翻折的題型

翻折折疊題型 (一) ，直接計算型，運用翻折的性質，結合題中的條件，或利用三角形相似，或利用勾股定理設方程來解題!一般難度小，我們要多做一些這些題型，熟練翻折的性質，以及常見的解題套路!

翻折折疊題型(二)，分類討論型，運用翻折的性質，結合題中的條件，或利用三角形相似，或利用勾股定理設方程來解題!一般難度較大，需要綜合運用題中的條件，多種情況討論分析，需要準確的畫圖，才能準確分析!

　　 歡迎使用手機、平板等移動設備訪問中考網，2023中考一路陪伴同行！>>點擊查看