來源:網絡資源 2023-02-02 20:30:12
列一元二次方程解決面積類問題
例1、如圖,某小區有一塊長為18米,寬為6米的矩形空地,計劃在其中修建兩塊相同的矩形綠地,它們的面積之和為60平方米,兩塊綠地之間及周邊留有寬度相等的人行通道。若設人行道的寬度為x米,則可以列出關于x的方程()
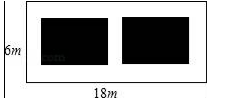
A.x2+9x﹣8=0B.x2﹣9x﹣8=0C.x2﹣9x+8=0D.2x2﹣9x+8=0
【解答】
解:設人行道的寬度為x米,根據題意得,
(18﹣3x)(6﹣2x)=60,
化簡整理得,x2﹣9x+8=0
故選C
例2、如圖,要設計一個等腰梯形的花壇,花壇上底長120米,下底長180米,上下底相距80米,在兩腰中點連線(虛線)處有一條橫向甬道,上下底之間有兩條縱向甬道,各甬道的寬度相等.設甬道的寬為x米。
(1)用含x的式子表示橫向甬道的面積;
(2)根據設計的要求,甬道的寬不能超過6米.如果修建甬道的總費用(萬元)與甬道的寬度成正比例關系,比例系數是5.7,花壇其余部分的綠化費用為每平方米0.02萬元,那么當甬道的寬度為多少米時,所建花壇的總費用為239萬元?

【解答】
解:(1)中間橫道的面積=(120+180)x=150x,
(2)甬道總面積為150x+160x﹣2x2=310x﹣2x2,
綠化總面積為12000﹣S花壇總費用y=甬道總費用+綠化總費用:
239=5.7x+(12000﹣S)×0.02,
239=5.7x﹣0.02S+240,
239=5.7x﹣0.02(310x﹣2x2)+240,
239=0.04x2﹣0.5x+240,
0.04x2﹣0.5x+1=0
編輯推薦:

歡迎使用手機、平板等移動設備訪問中考網,2023中考一路陪伴同行!>>點擊查看