來源:網絡資源 2023-03-14 21:23:40
因式分解是把一個多項式分解成幾個整式乘積的形式,它和整式乘法互為逆運算,在初中代數中占有重要的地位和作用,在其它學科中也有廣泛應用,學習本章知識時,應注意以下幾點。
1. 因式分解的對象是多項式;
2. 因式分解的結果一定是整式乘積的形式;
3. 分解因式,必須進行到每一個因式都不能再分解為止;
4. 公式中的字母可以表示單項式,也可以表示多項式;
5. 結果如有相同因式,應寫成冪的形式;

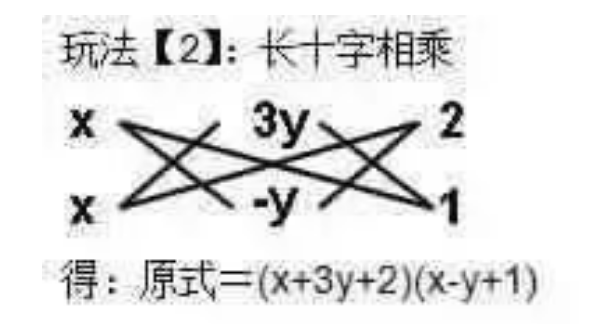
6. 題目中沒有指定數的范圍,一般指在有理數范圍內分解。1提公因式法簡單,不多說。ma+mb+mc=m(a+b+c)2運用公式法3分組分解法4十字相乘因式分解最好玩的部分。
簡單來講就是:十字左邊相乘等于二次項系數,右邊相乘等于常數項,交叉相乘再相加等于一次項系數。其實就是運用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆運算來進行因式分解。
二次項系數是1;
先請看下面一組因式分解:
x2-x-6=(x+2)(x-3)
x2+x-6=(x+3)(x-2)
x2-5x-6=(x+1)(x-6)
x2+5x-6=(x+6)(x-1)
仔細觀察上面的因式分解結果,你從中能悟出什么嗎?
我們知道因式分解是整式乘法的逆算,上述因式分解的依據是
(x+m)(x+n)=x2+(m+n)x+mn
我們知道常數項-6可以分解成
-6=-1×6=-6×1=-2×3=-3×2
又-1+6=5 所以x2+5x-6=(x+6)(x-1)
-6+1=-5 所以x2-5x-6=(x+1)(x-6)
-2+3=1 所以x2+x-6=(x+3)(x-2)
-3+2=-1 所以x2-x-6=(x+2)(x-3)

思考:當m為何值時,二次三項式x2+mx-6可以用十字相乘法進行因式分解?并用十字相乘法進行分解.
編輯推薦:

歡迎使用手機、平板等移動設備訪問中考網,2023中考一路陪伴同行!>>點擊查看