如果你也想進入數據分析的領域，那么統計學知識和概率論知識是必不可少的理論，雖然短時間你會覺得這個對碼代碼來說沒有什么用處，但是這個基礎還是要打好的，磨刀不誤砍柴工。

一、描述性統計

我想起了大學時候讀過，后期接觸專業課的時候反而不熟了。小學的時候都接觸過的平均數，標準差等等，我們真的有細細品味過其內涵嗎?

1.平均數

這個概念很簡單，一組數據的平均水平，但是平均數發現不了這組數據中“鶴立雞群”的數字。一個100分的學霸和4個70分的普通人平均一下，5個人的平均水平是76分，這無疑是對學霸的“褻瀆”，也沒有辦法發現這個“骨骼驚奇”的人類了。

2.中位數、眾數、四分位數、箱線圖、直方圖

中位數可以發現這組數據的中間水平，眾數即為大眾水平，四分位數得到的箱線圖和中位數結合來看，可以得到大部分人的水平，以及優劣的集中程度。

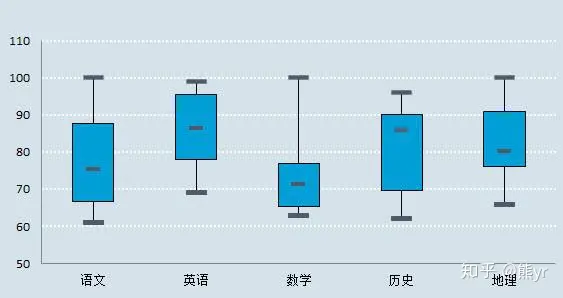
如上圖，數學箱線圖里我們可以看出這個班級數學最高分有100，最低分63左右，歷史最高分不到100，最低分低于數學。但是我們能說歷史的成績要不如數學嗎?數學的箱體偏下，中位數居中，說明數學雖然有100的學霸，但優秀者鳳毛麟角，一半人還是處于80到60 之間。而歷史成績，則在98到62范圍內更均勻，而且中位數88左右在箱體偏上部分，說明有一半人在88以上，88到90的人有四分之一。同理對于地理來說雖然中間部分集中情況優于數學，但是四分之一的人集中在76到80，明顯不見得比歷史好。

箱線圖相當于是中位數、眾數、四分位數在圖像上更為直觀的反映，因為我們大腦對于圖像理解更為快速。箱線圖可以讓那些“鳳毛麟角”凸顯出來，相比于平均數更能凸顯異常者。

(這里想請教一下MAC版EXCEL2016怎么畫箱線圖，怎么用股價圖來畫)

直方圖也是差不多的用途，直方圖在數據上更為精確，能夠通過頻率和范圍直接計算出頻數，而箱線圖則表示不出來，而且直方圖能更直觀的感受數據的分布情況。但是直方圖在多組數據同時表示時則相對來說比較復雜，一組數據需要一個直方圖，箱線圖則不會占據較大的篇幅。

3.標準差、夏普比率

標準差，大家都能理解就是穩定程度。作為一個金融渣，時隔幾年終于深層次理解了曾經投資課聽不懂的夏普比率，這說明我確實沒有自己想象的那么學霸。

如果我們不是靠背誦知道的標準差代表穩定程度，僅僅從公式理解上，即為這一組數據里每一個數字與平均值的差距。那么在投資上代表風險，即為某一種投資，相對于平均值我可能賠也可能賺。那么再來理解夏普比率，某一種投資組合的投資回報減去無風險回報后的溢價與標準差的比值。假如夏普比率為0.5，意思是我在賺0.5份溢價的時候可能承擔的風險是賺1份或者賠1份的風險。(鄙人粗見，歡迎指正)

4.標準分

表示離平均值的差距是標準差的幾倍。我是這么理解的：全體考生的標準差相當于全體考生的集散程度，而個體的標準分相當于這個個體偏離“組織”的程度。如果整體的標準差很大，我即使偏離平均很多，我也不見得離組織很遠，因為大家都離得遠。但是如果整體標準差不大，我如果稍微比平均值差一些很可能就偏離組織了。標準分的正負說明我是在平均以上還是以下，標準分的絕對值說明我離“組織”的距離相對于整個組織的離散程度是更離散還是還好。

標準分和標準差的區別在于標準差是整體的離散程度，而標準分是針對個體的離散程度和整體離散程度的相對效果。

二、概率

1.乘法公式

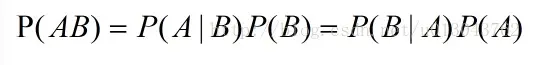
第一個是乘法公式，第二個是條件概率公式。

當且僅當兩個隨機事件A與B滿足P(A∩B)=P(A)P(B)。

2.全概率公式

3.貝葉斯公式

貝葉斯公式的理解：假設i=2，我們知道有兩種方法以及選擇每種方法的概率，同時我們知道每種方法都會導致結果B且只有這兩種方法會導致結果B，我們又知道兩種方法分別導致結果B的概率。現在結果B出現了，我們怎么確定某一種方法導致結果B的概率。這里先驗概率就是已知條件，后驗概率就是結果出現后我們想知道這個結果由某一種方法導致的概率。

4.大樹定律

當統計數量足夠大，那么事物出現的頻率就能無限接近他的期望。如果數量很小，那么事物出現與其期望值一點關系都沒有。

三、決策樹分析目前個人工作情況

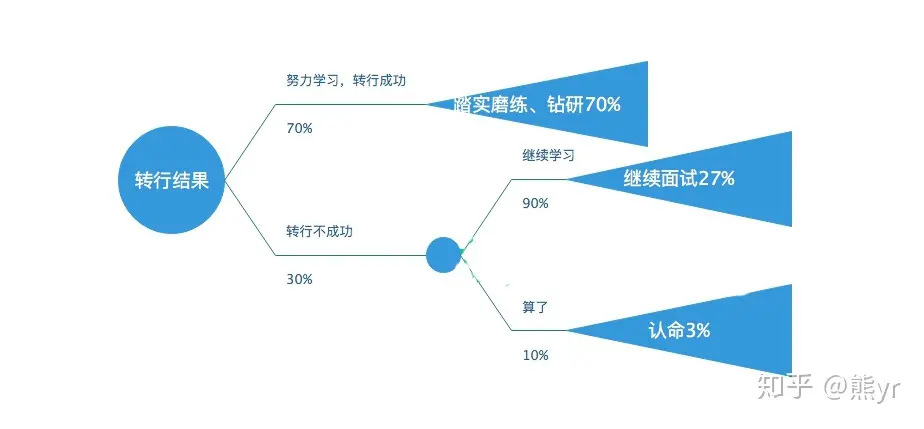
鑒于本人對于目前工作情況并不滿意，原因主要是三個：一、我需要一個有雙休的工作，工作時間不規律讓我很不適應，身體素質也因為忙碌的三個月下降了不少。二、我性格不適合營銷，我喜歡不停的鉆研，自己思考，作出成果。三、目前公司的文化不認同。所以我沒有什么是否需要轉行的考慮。只有是否能轉行成功的考慮，我很怕因為年齡和經驗的問題而不被認可。但是基于我對公司的認同度的極速下滑，我還是有必要轉行。但是目前困難已經出現了，我搜索引擎使用的不是很好，特別是爬蟲翻墻挖掘數據有一定的困難。另外MAC版的軟件用起來和window還是差別很大，不是很方便。

       編輯推薦：

       2023年中考各科目重點知識匯總

　　 歡迎使用手機、平板等移動設備訪問中考網，2023中考一路陪伴同行！>>點擊查看