來源:網絡資源 2023-06-28 17:03:19
點的坐標特征
01
第一象限內的點橫坐標為正,縱坐標為正,即(+,+);第二象限內的點橫坐標為負,縱坐標Wie正,即(—,+);第三象限內的點橫坐標為負,縱坐標為負,即(—,—);第四象限內的點橫坐標為正,縱坐標為負,即(+,—)。
例題1:若點A(a+1,b-2)在第二象限,則點B(-a,1-b)在第( )象限。
解:∵點A(a+1,b-2)在第二象限,
∴a+1<0,b-2>0,
解得:a<-1,b>2,
則-a>1,1-b<-1,
故點B(-a,1-b)在第四象限
解此類問題的一般方法是根據點在坐標系的符號特征,建立不等式(組)或方程(組),把點的問題轉化為不等式(組)或方程(組)來解決。
點的平移與對稱
02
左右平移,改變的為點的橫坐標。點(x,y)向左平移a個單位,得到的點坐標為(x-a,b),向右平移b個單位,得到的點坐標為(x+b,y)。上下平移,改變的為點的縱坐標。點(x,y)向上平移a個單位,得到的點坐標為(x,y+a),向下平移b個單位,得到的點坐標為(x,y-b)。
例題2:已知線段CD是由線段AB平移得到的,點A(-1,2)的對應點為C(3,1),則點B(-2,-2)的對應點D的坐標為( )
解:由點A(-1,2)的對應點為C(3,1),知線段AB向右平移4個單位、向下平移1個單位即可得到CD,
∴點B(-2,-2)的對應點D的坐標為(-2+4,-2-1),即(2,-3),
關于x軸對稱的點,橫坐標相同,縱坐標互為相反數;關于y軸對稱的點,縱坐標相同,橫坐標互為相反數;關于原點對稱的點,橫、縱坐標都互為相反數。
例題3:將三角形三個頂點的橫坐標都乘以-1,縱坐標不變,則所得三角形與原三角形的關系是
解:由題意,橫坐標互為相反數,縱坐標不變,那么兩個圖形關于x軸對稱。
變式:將三角形三個頂點的橫坐標都減2,縱坐標不變,則所得三角形與原三角形的關系是
解:∵將三角形三個頂點的橫坐標都減2,縱坐標不變,
∴所得三角形與原三角形的關系是:將原圖向左平移兩個單位.
在平面直角坐標系內,把一個圖形各個點的橫坐標都加上(或減去)一個整數a,相應的新圖形就是把原圖形向右(或向左)平移a個單位長度;如果把它各個點的縱坐標都加(或減去)一個整數a,相應的新圖形就是把原圖形向上(或向下)平移a個單位長度.(即:橫坐標,右移加,左移減;縱坐標,上移加,下移減)
位置的確定
03
由已知條件建立合適的直角坐標系的關鍵是:(1)要正確確定坐標原點的位置;(2)要準確確定單位長度。
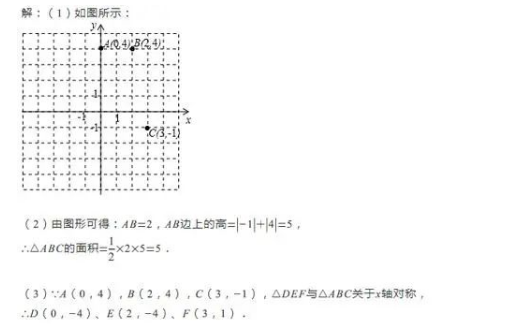
例題4:平面直角坐標系中,△ABC的三個頂點坐標分別為A(0,4)B(2,4)C(3,-1).
(1)試在平面直角坐標系中,標出A、B、C三點;
(2)求△ABC的面積.
(3)若△DEF與△ABC關于x軸對稱,寫出D、E、F的坐標.
分析:(1)根據三點的坐標,在直角坐標系中分別標出位置即可.(2)以AB為底,則點C到AB的距離即是底邊AB的高,結合坐標系可得出高為點C的縱坐標的絕對值加上點B的縱坐標的絕對值,從而根據三角形的面積公式計算即可.(3)關于x軸對稱的點的坐標,橫坐標不變,縱坐標互為相反數,從而可得出D、E、F的坐標.
本題考查了坐標與圖形性質,軸對稱作圖,三角形的面積,解答本題的關鍵是正確的找出三點的位置,另外要掌握關于x軸對稱的點的坐標的特點。
規律探究
04
以循環為特征的規律探索型問題,解決此類問題應先觀察圖形的變化趨勢,然后對第一個圖形進行分析,運用從特殊到一般的探索方式,如果以m次為一個循環,那么第n次的情形與n÷m的余數是相同的,整除時與最后一次情形相同。
例題5:如圖,直角坐標平面xOy內,動點P按圖中箭頭所示方向依次運動,第1次從點(-1,0)運動到點(0,1),第2次運動到點(1,0),第3次運動到點(2,-2),…按這樣的運動規律,動點P第2020次運動到點( )
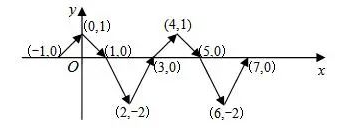
分析:觀察圖形可知,每4次運動為一個循環組循環,并且每一個循環組向右運動4個單位,用2020除以4,然后根據商和余數的情況確定運動后點的坐標即可.
解:∵2020÷4=505,
∴動點P第2020次運動為第505個循環組的第4次運動,橫坐標505×4-1=2019,縱坐標為0,
∴點P此時坐標為(2019,0).
平面直角坐標系下的規律探究題,解答時注意探究動點的運動規律,又要注意動點的坐標的象限符號。
編輯推薦:

歡迎使用手機、平板等移動設備訪問中考網,2024中考一路陪伴同行!>>點擊查看